Associative
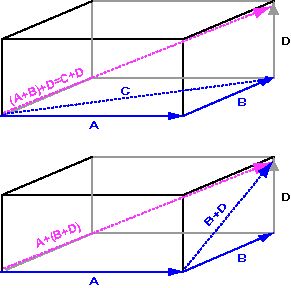
The top diagram shows the result of adding
(a + b) + d = c + d.
The result is the vector with length and direction
the same as the diagonal of the figure.
The bottom diagram shows the result of adding
a + (b + d).
The result is the same.
This is a demonstration of the
associative property of vector addition:
a + (b + c) = (a + b) + c
The rule works in all dimensions.
Mostly the geometric vectors of
computer graphics are
two dimensional and
three dimensional
(although, in general,
higher dimensions are possible).
The associative property means that sums
of several vectors can be
written like
a + b + c + d + e
without parentheses.
QUESTION 6:

Say that you walk five blocks north, and then three blocks east.
If, instead, you had walked
three blocks east
and then five blocks north
would you arrive at the same place?

