Published:
March 25, 2007
Last Updated: October 26, 2007
By Richard G. Baldwin
Alice Programming Notes # 900
This document serves as an appendix to a series of programming tutorial lessons that are designed to teach you how to program using the Alice programming environment under the assumption that you have no prior programming knowledge or experience.
The purpose of this appendix is to explain and to illustrate the behavior of the twenty primitive methods that belong to all, or at least most Alice objects.
I recommend that you open another copy of this document in a separate browser window and use the following links to easily find and view the figures, listings, and tables while you are reading about them.
Once you have mastered Alice, I recommend that you also study the other lessons in my extensive collection of online programming tutorials. You will find a consolidated index at www.DickBaldwin.com.
The purpose of this document is to provide reference material explaining and illustrating the behavior of the twenty primitive methods that belong to all, or at least most Alice objects. Before doing that, however, I will need to provide some general background information about the construction of programs in Alice.
Computer programs accomplish what they accomplish by performing operations on data. For example, a banking program performs operations on a variety of different kinds of data such as account balances, deposits, etc.
The primary kinds of data that are used in Alice programs are the following:
(If I omitted any important kinds of Alice data, please send an email telling me what I omitted.)
|
In a manner similar to the way that animals are subdivided into dogs, cats, tigers, bears, etc., data is subdivided into types. The primary types in Alice are:
A class is a blueprint or plan from which one or more identical objects can be constructed. This is similar to constructing several condominiums from a single set of blueprints or plans. Frequently a condo starts out being identical to other condos in the project. However, you can customize your condo if you choose by painting it a different color, putting down different carpet, etc.
In a similar manner, even though all objects constructed from a given class start out being identical, you can customize them by causing their property variables (such as the color property) to have different values.
The Local Gallery and the Web Gallery in Alice contain perhaps a thousand or more different classes that can be used to construct objects. Those classes describe things like penguins, flashlights, parking meters, etc. In addition, you can extend or customize those classes to create new classes of your own design.
In object-oriented programming jargon, an object is an instance of a class. In other words, a single object is the product that results from constructing a single instance of the thing that the class (blueprint or plan) describes. For example, a condo is a single instance of the blueprint that is used to construct several initially identical condos.
Any number of identical instances (objects) can be constructed from a single class. Once an object has been constructed, it can be customized by assigning different values to the object's property variables.
Just like plants and animals, objects have behavior. A method is the mechanism by which the program sends a message to an object asking it to execute one of its behaviors. For example, the method named move, when executed on an Alice object, will cause the object to move a prescribed distance in a prescribed direction in the 3D world represented by an Alice program.
Just like newborn babies, when a new object is created, it already has a set of behaviors that it knows how to execute when asked to do so. Figure 1 contains a list of the twenty primitive methods belonging to all (or at least most) Alice objects.
Figure 1. Alice primitive methods.
Alice primitive methods
|
A shortage of documentation on primitive methods
As of the date of this writing, I have been unable to find a single document that explains the behavior of these primitive methods anywhere on the web. The main purpose of this appendix is to explain, and in most cases to illustrate, the behaviors that these primitive methods impart to the object to which they belong.
Method names are important but not sufficient
In some cases the method names clearly indicate the imparted behavior. However, in other cases, the method names are ambiguous with regard to imparted behavior. For example, the differences in behavior imparted by the methods named turnToFace and pointAt are very subtle. Sometimes, either method will suffice for a particular purpose, but sometimes that is not the case.
The method named moveAwayFrom
Similarly, the behavior imparted by the method named moveAwayFrom is also ambiguous. We can surmise that this method will cause one object to move away from another object, but in what direction? Will the object move forward, backward, or sideways? If sideways, will it move to the right or to the left? You will find the answers to many questions like this in this appendix.
The method named turn
At first glance, the method named turn seems straightforward enough. However, when you write code to cause an object to turn, you must select one of the following method parameters:
Experienced programmers can probably figure out what it means to turn LEFT or RIGHT but that is not necessarily true for an aspiring programmer with no programming experience. Even an experienced programmer may have some difficulty figuring out what it means to turn FORWARD or BACKWARD since those two terms have a different meaning with regard to the Alice turn method than they typically have in everyday life.
The turn method versus the roll method
As another example, what is the difference between telling an object to turn RIGHT or to roll RIGHT? Once again, an experienced 3D graphics programmer could probably figure this out, but an experienced programmer whose programming background is mainly in the business and database area may have some difficulty with this one.
Take the mystery out of the methods
In this appendix, I will take the mystery out of the behavior of the twenty primitive methods. Be aware, however, that because I haven't found any real documentation on the primitive methods, the information that I will provide in this appendix will be based solely on my experimentation. This experimentation may fail to identify some of the subtleties in the behavior imparted by some of the methods. If you discover that any of my explanations are inaccurate or incomplete, please send an email message advising me of that fact.
In addition to the primitive methods, some of the classes in the Local Gallery provide custom methods. For example, an object constructed from the Penguin class has the following custom methods in addition to the primitive methods:
There are subtleties in the behavior imparted by some of the custom methods as well, but I won't attempt to explain custom methods in this appendix. For example, what is the difference between the method named walk and the method named walking? Maybe that will be another task for another day.
In addition to the primitive methods and the custom methods, it is also possible for you as the programmer to add your own new methods to an object. I mention this here only for completeness, as that is a topic that will not be addressed in this appendix at all.
|
A method parameter (sometime called a parameter variable) is the mechanism by which you provide information to the method when you send the message to the object asking it to execute the behavior imparted by that specific method. We commonly refer to this as passing a parameter to the method.
Required parameters
A review of the Alice development screen reveals that all but one of the primitive methods requires one or more parameters to be passed to the method when it is called. Typical parameters are directions, amounts, etc. (The method named standUp doesn't require any parameters, but there are default parameters even for this method.)
Default parameters
Default parameters are those parameters for which default values are already established, but for which you may provide values that are different from the default if you elect to do so. Each primitive method has several default parameters. Each default parameter has several allowable values. (See Table 1 for an example.) Obviously, I won't be able to explain how they all impact the behavior of a primitive method in this document, but I will try to explain some of the most commonly used default parameters.
Specifying default parameter values
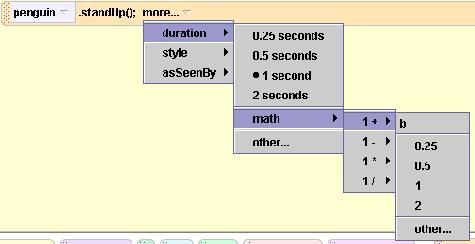
Figure 2 shows a (cropped and somewhat reduced) screen shot showing the mechanism by which default parameter values are specified.
Figure 2. Screen shot showing default parameters.
 |
To specify a default parameter, you click on one of the little triangles that point down in the program instruction. This causes a cascade of popup menus to appear from which you make your selection. For those cases where the parameter value is a numeric value and the value that you need isn't one of the visible choices, you can select a menu item labeled other. This will pop up something resembling a calculator keyboard, which you can use to specify any numeric value.
The behavior imparted by many of the primitive methods causes the object to take some action relative to Alice's 3D world, and the 3D coordinate system that describes that world. Therefore, in order to understand the behavior of many of the methods, you must first understand the coordinate system.
I discuss these issues in much more detail in another lesson titled "Learn to Program using Alice, Objects in 3D Space" (see Resources). Therefore, the material on this topic in this appendix will primarily be a recap.
What happened to the X, Y, and Z coordinate system?
Historically, programmers working in 3D space have considered 3D space to be described by three orthogonal axes, typically referred to as X, Y, and Z. However, the developers of Alice have gone out of their way to avoid this nomenclature. The 3D space in an Alice program is still represented by three orthogonal axes, but directions in Alice are commonly described as RIGHT, LEFT, UP, DOWN, FORWARD, BACKWARD, etc.
|
Just about everything in Alice, including the world is an object. Every object in Alice has a center point and has its own set of three orthogonal axes. The center point is the single point in or near the object where the three orthogonal axes cross. This would be referred to as the origin in other programming environments.
Moving and rotating an object
When you move an object, you move its center point. All three of its orthogonal axes come along for the ride. When you rotate an object around one of its axes, the orientation of that axis stays the same but the orientations of the other two axes change.
Illustrate the axes with pictures
I will illustrate the Alice coordinate system using a series of pictures. I don't know of any way to directly display the axes that describe the world, but it is relatively easy to display the axes of any other Alice object. All you need to do is to select the object in the object tree while operating in the scene editor mode (as opposed to code editor). However, there is an indirect way to display the axes of the world, and the result is shown in Figure 3.
Figure 3. The axes of the world.

|
|
Figure 3 shows a world where the ground is covered with snow. This is convenient because I needed a white background to show you what I need to show you.
Displaying the ground object's axes
For Figure 3, I called the primitive method named setPointOfView on the ground object to cause its viewpoint to be aligned with the viewpoint of the world object. In other words, I caused the center point of the ground to match the center point of the world, and caused the ground to have the same orientation as the world. Then I selected the ground in the object tree to cause its three axes to be displayed. The three axes shown in Figure 3 overlay the three corresponding axes of the world.
The red, green, and blue axes
Even though it may not seem to make sense in some cases, every Alice object has a front, back, right, left, top, and bottom. The blue axis shown in Figure 3 always points in the direction looking out from the front of the object (the direction that the headlights on an automobile shine).
The red axis in Figure 3 always points in the direction looking out from the right side of the object (the direction that you point if you extend your right arm directly out from the right side of your body).
The green axis always points in the direction looking out from the top of the object (the direction that I look when I look out of the sun roof of my car).
In the more conventional notation used in other 3D programming systems, I believe we would say that red equates to X, green equates to Y, and blue equates to Z.
Does the ground have a front and a back?
If we stand on the ground and look around in the real world, we would probably agree that the ground has a top. Does it have a bottom? It doesn't make a lot of sense in the real world to talk about the right side, left side, front, back, and bottom of the ground. Nonetheless, the ground is an object in Alice. Those concepts apply to the ground (and all other objects) in Alice and the coordinate system for the ground is based on those concepts.
A flashlight aligned with the world
To get a little closer to something that makes more sense in the real world, Figure 4 shows a flashlight for which the viewpoint of the flashlight has been aligned with the viewpoint of the world.
Figure 4. A flashlight aligned with the world.

|
|
With the flashlight, the concept of the front and the back makes a lot of sense, but since a flashlight is typically a cylindrical tube, the concept of the right side, left side, top, and bottom doesn't necessarily make sense. Once again however, they exist for the flashlight in Alice and the coordinate axes for the flashlight shown in Figure 4 are based on those concepts.
Where is the bottom half of the flashlight?
Note that the flashlight shown in Figure 4 is half buried in the snow. This is because the center point of the ground (the snow) is at the surface of the snow. The center point for the flashlight is in the middle of the flashlight. Therefore, once the viewpoints of the two objects are aligned, half of the flashlight is on the top of the ground and the other half is protruding from the bottom of the ground. (The ground in Alice is a very thin sheet with open 3D space underneath.)
What about the yellow lines?
At this point in the discussion, you should simply ignore the faint yellow lines in Figure 4 and Figure 5. They have no bearing on this discussion but I had no way to eliminate them from the images. I will explain what they are later.
Flashlight moved and rotated
Figure 5 shows the result of first driving a stake through the original center point of the flashlight to serve as a visual reference, and then moving and rotating the flashlight.
Figure 5. Flashlight moved and rotated.
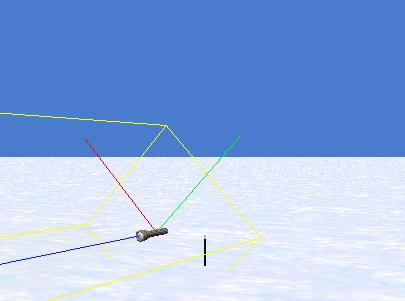
|
The flashlight was moved forward, to the right, and up by one-half meter in each of those three directions. Then it was rotated to the left (around the blue axis) by 45 degrees.
Note first that the center point of the flashlight, along with the three axes, moved along with the entire flashlight. Note also that the orientation of the blue axis did not change, but the red and green axes were both rotated around the blue axis by 45 degrees. This moving and rotating of the flashlight was accomplished by calling the move method three times in succession followed by calling the roll method once.
Two more pictures regarding the coordinate system
I have two more pictures to show you to help clarify the concept of an object having a front, back, right, left, top and bottom. Figure 6 shows a penguin standing on the ground where the viewpoints of the penguin and the ground have both been aligned with the viewpoint of the world.
Figure 6. Penguin aligned with the world showing ground's axes.

|
In Figure 6, the ground was selected in the object tree to cause its axes to be visible. As you can see, the blue axis points out in front of the penguin (along the surface of the ground), the red axis points out to the right of the penguin, and the green axis points up and out of the top of the penguin's head.
Now display the penguin's axes
Figure 7 shows the same world, but with the penguin selected in the object tree to cause its axes to be displayed.
Figure 7. Penguin aligned with the world showing penguin's axes.

|
Although they are more difficult to see because they are shorter, the red, green, and blue axes belonging to the penguin overlay the red, green, and blue axes belonging to the ground. Both of those sets of axes also overlay the corresponding axes belonging to the world, but we have no way to show that. (They overlay only because the viewpoints of all three objects were aligned.)
A penguin's belly is in the front
A penguin does have a front, back, right side, left side, top, and bottom, so in the case of a penguin (unlike the case of the ground and the flashlight), those concepts make very much sense in terms of what we know about the real world. However, the important point is that even if it doesn't seem to make sense in terms of what we know about the real world, every object in Alice has a front, back, right, left, top, and bottom. Every object also has a red axis, a green axis, and a blue axis, and they point in the directions of right, up, and front respectively.
The center point for the penguin
Note the center point for the penguin is not actually inside the penguin. Rather, it is half way between the penguin's feet at the level of the soles of the penguin's feet. (This is the point in 3D space where all three axes meet.)
What about the yellow lines?
This will also be an opportune time to provide a little information about the yellow lines that I mentioned earlier. As you may be able to see in Figure 7, they form the edges of a rectangular 3D box. This box is often referred to as the bounding box for the object, and its size is such as to enclose the entire object. The box has a height, a width, and a depth. These values can be accessed on any object using program code.
If you go back and look at Figure 5, you will note that the bounding box is much larger than the flashlight. That is because the flashlight object also includes a cone shaped light beam that extends far out in front of the flashlight and becomes very wide at a point at some distance from the flashlight lens. However, the light beam isn't very bright and can't be seen against the white background in Figure 5. The light beam is included in the bounding box for the flashlight.
In the following sections, I will explain and illustrate the behavior of the twenty primitive methods that belong to all, or at least most Alice objects.
|
Will provide sample code
In many cases, in addition to providing a verbal explanation of the behavior, I will also provide the source code for one or more short programs that you can write to see the behavior in action. I have also provided a zip file containing the Alice a2w files for each of the sample programs (see Downloads). You can download those files and run them in your Alice 2.0 environment.
Also, in some cases, I will walk you through a series of manual interactive method calls that demonstrate the behavior of the method being discussed. (See setPointOfView for example.)
Creating your worlds
In some cases, I will also explain what you need to do to create the world necessary to write the program, such as which objects to place in the world, before you begin writing code. However, in most cases, that should be obvious so I will omit the setup instructions in most cases. In those cases, if you can't figure out how to create the world, you can download the program and open it in your Alice environment.
Houston, we have a problem!
My objective is to make it possible for you to reproduce my results exactly. Therefore, I normally won't ask you to make manual adjustments to the size, orientation, or position of an object simply by dragging the mouse. However, there is one situation that can cause us to get different results over which I have no control.
The lens angle slider
When the Alice development environment is in the Scene Editor mode, it is possible to expose a slider near the upper right corner of the screen labeled "lens angle." If you change the position of that slider, you will get a different view of the world.
If we each play the world without having that slider in the same position, the objects on your screen will be either larger or smaller than the objects on my screen. In addition, our two cameras will have different field widths. This is essentially a manual zoom control. As far as I know, there is no way to control this zoom factor under program control, so there is no way to guarantee the repeatability of the visual aspects of a program.
Just so you will know, I normally operate my system with that slider about one-eighth of the way from the left end and keep the slider hidden so that I won't accidentally change it. However, if your objects appear larger or smaller than mine, try adjusting that slider to see if you can cause them to be approximately the same size.
The order of the method descriptions
For your convenience in using this document as reference material while writing your Alice programs, I have arranged the explanations of the methods in the same order that they appear in the methods tab of the details panel in the Alice development environment. This is also the order that they appear in the Table of Contents.
However, that isn't necessarily the best order for you to study the behavior of the methods. Also, that isn't necessarily the best order for me to write the explanations. I will write the explanations in a different order than the order in which the methods appear in this appendix. This will result in the figures and the listings not necessarily being in numeric order. However, you will find an index to all of the figures and the listings here. That index is in numeric order.
You will find an index to all of the methods in the order that they appear in the methods tab of the Alice details panel here. Just select a method name and click on it to jump to the section of the appendix in which the method is explained.
You will also find an index to all of the methods in the order that I recommend that you study them (the recommended study trail) here.
The recommended study trail
To help you in your efforts to study the material in this appendix, I have marked out my recommended trail through the various sections that explain the methods. I refer to this as the recommended study trail. At the end of each section that explains a method, I have provided a hyperlink to the method that I recommend you study next. At the beginning of each section that explains a method, I have provided a hyperlink back to the previous lesson on the recommended study trail.
Of course, you should feel free to study this material in whatever order works best for you.
The points on a compass
One way to think about the Alice 3D world is to think of the plane described by the red and blue axes as the surface of a flat earth, with the green axis pointing straight up into the sky.
If we think of it that way, then the blue axis points toward the south and the red axis points toward the west. This makes it a little easier to talk about and to explain what we are doing in some cases.
The front of the world faces south
Given this convention, it can be shown through experimentation that he "front" of the world faces south, whatever that means.
However, what it means becomes clearer when we align the viewpoint of another object with the viewpoint of the world. The front of the new object will also face south.
The penguin is facing south
When considered in this manner, the penguin shown in Figure 6, (whose viewpoint was aligned with the viewpoint of the world), is facing south. If he were to raise his right wing, it would be pointing west.
Feel free to jump around
You should feel free to jump around and study the explanations of the methods in whatever order makes the most sense to you. Be aware, however that unlike a true documentation package (such as the Java API documentation from Sun) the descriptions of the methods in this document are not independent of one another. In other words, the discussion of a particular method will frequently refer back to, or perhaps depend upon a previous discussion of a different method and those discussions are not intended to stand alone. Therefore, you may get more out of the material if you follow my recommended study trail and study the method descriptions in the order that I recommend, at least during your first pass through the methods.
|
I will be using the method named setPointOfView extensively from the beginning of the discussion so that would be a good place for you to begin studying the behaviors of the primitive methods. Therefore, I recommend that your first stop on the recommended study trail be the section that explains the method named setPointOfView.
This section contains a link to the explanation of each of the primitive methods in the order that I recommend that you study them.
Recommended study trail: Return to the explanation of the method named setPointOfView.
Brief description: A method to cause an object to be moved in a specific direction by a specific distance.
A fairly simple method
The move method is one of the simplest of all the primitive methods, particularly if you don't change any of the default parameter values.
Because of the simplicity of the method, it will provide us with a good opportunity to illustrate changes in two of the default parameters and to discuss a third default parameter. Those three default parameters are:
Writing the program named move01
The source code for my version of a program named move01 is shown in Listing 1 near the end of the lesson. You can also download a completed version of the program.
Create a new world
To write your own version of the program, create a new world, select the snow template, add a penguin from the Animals subsection in the Local Gallery to the world and save the world as move01.
The main method
Change the name of the default startup method to main. All of the code in the program will be contained in the main method.
Six lines of comments
The program begins with six lines of comments. I placed those comments in a doInOrder construct so that I could collapse them into a single line during editing to save space and eliminate congestion on the edit screen.
Initializing the viewpoints of the objects
Most of the code in this program is used to initialize the viewpoints of all the objects to known repeatable viewpoints. This should make it possible for you to replicate the program and have it produce the same results.
Initializing the viewpoint of the camera
The next major block of code is the code in the block under the comment that reads "Set viewpoint of the camera." That block of code sets the viewpoint of the camera. I also placed this code in a doInOrder construct for the same reason given above. You will see that I almost often do this.
The camera code begins by calling the setPointOfView method to cause the viewpoint of the camera to be aligned with the viewpoint of the world. The purpose for making this method call is to cause the camera to start off with a known viewpoint. As I mentioned earlier, this causes the camera to be facing south. Assuming that the center point of the camera is at the center of the lens, it also means that half of the lens will initially be buried below the surface of the ground. This is because the center point of the ground, which will later be aligned with the viewpoint of the world, is at the surface of the ground.
Required parameters for the move method
The move method requires only two parameters:
The allowable values for the direction parameter are:
|
If you want to cause the object to move in some direction that is not included in the above list of allowable values, you must make either two or three separate moves, the result of which will resolve to the desired direction and distance. Note however that because of the doTogether construct provided by Alice, the fact that you have specified three separate moves to accomplish a single move won't necessarily be apparent to the viewer.
|
Allowable values for the amount
The allowable value for the amount can be anything you want it to be as long as you can express the amount in meters or fractional parts thereof. You can even specify a negative value for the amount, which will effectively reverse the specified direction of the move. (In some cases, negative values for the distances can be used to reduce the required number of instructions in a program.)
The duration parameter
This will be an opportune place to discuss the parameter named duration. This is one of the default parameters mentioned earlier. You will see a value of 0 for that parameter being passed to the setPointOfView method in every one of the method calls in the block of code that was used to set the viewpoint of the camera in Listing 1.
A default value of one second
This parameter has a default value of one second. That means that if you don't specify the value of this parameter when you make the method call, the method will require one full second to complete, even if the computer can complete the action much more quickly.
Animation speed is often lower than computer speed
When we make method calls to animate an object, we often slow the action down to the point that a human observer will be able to see and understand what is happening. The intended purpose of the duration parameter is to allow us to control the elapsed time for every action that we ask an object to perform. We can set the value of the parameter to any amount of time in seconds, including fractional parts of seconds or zero. (Negative values seem to be treated the same as 0.)
Don't want to slow down the initialization of the viewpoints
Since the method calls that were made on the camera object are there for the sole purpose of setting the initial viewpoint of the camera, we would like for them to be completed as quickly as possible. Therefore, the value of the duration parameter was set to 0 for every method call that was made on the camera. This means that the action will be performed and the method will return as quickly as the computer is capable of performing that action.
Think about the viewpoint of a camera
Now think for a moment about the viewpoint of a camera. If you are taking pictures and your subjects are facing south, the camera needs to be facing north. In other words, the front of the camera needs to be facing the subjects (even if the subjects are not facing the camera). Also, the camera usually needs to be several feet above the ground, and several feet away from the subjects. The remaining four method calls that were made on the camera in Listing 1 were designed to accomplish those two purposes.
Calling the turn method
The statement that calls the turn method with one parameter value of LEFT and a second parameter value of 0.12 revolutions causes the camera to rotate to the left around its green (vertical) axis by 45 degrees. This causes the camera to be facing toward the southeast. (I will have much more to say about the turn method in the section that explains that method.)
Move forward, turn again, and raise the camera
The call to move the camera FORWARD by 20 meters does just that. It moves the camera without changing its orientation.
The call to turn the camera to the LEFT by 0.5 revolutions causes the camera to end up facing towards the northwest.
The call to move the camera UP by 2 meters causes the camera to be elevated above the ground by 2 meters without changing its orientation. (Obviously, this is not the only way, or even the most compact way to set the initial viewpoint of the camera.)
The camera has a known viewpoint
At this point in the program, the camera has a known viewpoint. In a more complicated animation program, this known viewpoint can serve as the starting viewpoint for the camera. The camera's viewpoint may be adjusted many times during the remainder of an actual animation program. However, because the camera starts with a known viewpoint, the program can use that known viewpoint in conjunction with the known values of all subsequent viewpoint adjustments to know exactly what the current viewpoint of the camera is throughout the remainder of the program execution.
Play the world
If you download this program and play the world, you will see this camera movement taking place very quickly, but not quickly enough to make it invisible to a viewer. In fact, the camera motion can be somewhat annoying to the viewer.
|
In addition to causing the initial viewpoints of the objects to be set very quickly (by setting the duration parameter value to 0), it is also a good idea to set the isShowing property value of all the objects to false (make them invisible) before executing this initialization process for setting the viewpoints. Otherwise, you will probably see some undesirable flashing on the screen.
Set viewpoints of the ground and the penguin
The next two statements in Listing 1 call the setPointOfView method twice in succession for the purpose of aligning the viewpoints of the ground and the penguin with the viewpoint of the world. Once again, the value of the duration parameter was set to 0 in both cases to cause this to happen very quickly.
Now begin the animation
In an actual animation program, this is the point in the program where I would start making objects visible and calling methods on them to control their behavior (to animate the objects). In this program, the animation is very simple. The penguin is moved RIGHT by 10 meters with a duration of 2 seconds. Then the penguin is moved LEFT by 10 meters also with a duration of 2 seconds. When the program ends, the penguin is back at his initial position.
Using the style parameter
However, the second movement is not simply the reverse of the first movement. Another default parameter named style is used to control some of the fine details regarding the movement in each direction. This parameter specifies how the object will start and end the motion. The allowable values are:
Option 1 is the default value
When the penguin moves to his RIGHT in Listing 1 without me having set a new value for the style parameter, the movement behaves according to the first option in the above list of allowable values.
Try option 4
The fourth option was specified for the style parameter when the penguin moved back to his LEFT in Listing 1.
Can you see the difference?
If you download and run this program, you should see the penguin move to his RIGHT and then move back to his left. It will be interesting for you to see if the motion in one direction looks any different from the motion in the other direction on your computer. On my computer, (which is fairly slow), the motion is not very smooth in either direction, so it is difficult for me to tell the difference between the two styles. You might try changing the value of the duration parameter in both statements to see if that makes the difference between the two styles easier or more difficult to see.
A case where the different styles can be seen
The situation where I have noticed that the style has the greatest visual effect is where one motion leads directly into another motion and it is desired that the two motions fuse together to look like a single smooth motion.
With option 1 or 3 (END_GENTLY) for the first motion, or option 2 (BEGIN_GENTLY) for the second motion, you can sometimes see what appears to be a slight undesirable pause at the end of the first motion and the beginning of the second motion. This is a case where ending the first motion ABRUPTLY and beginning the second motion ABRUPTLY seems to work best.
|
The asSeenBy property
There is another default parameter named asSeenBy, which comes up often, and which can be used to create very interesting effects. I believe that the default value for this parameter is normally <None> but the allowable values are all of the objects in the world, including the world, the camera, and the light.
For example, there are two calls to the move method at the end of the program named move01 as shown in Listing 1. The first call tells the penguin to move to its RIGHT (the direction of its red axis) by 10 meters. The second call tells the penguin to move to its LEFT by 10 meters. When you play the world, you see the penguin move first to its right followed immediately by a movement to its left.
|
If you were to modify those two method calls to set the value of the parameter named asSeenBy to the camera, and leave the directions of movement the same, you would see the penguin move first to its left (which is the camera's right), followed by a movement to the penguin's right (which is the camera's left).
A little more on the parameter named asSeenBy
Many of the primitive methods support the default parameter named asSeenBy, and the effect of setting the value of this parameter to some object other than the object on which the method is being called will depend on the specific behavior of the method involved. However, I want to give you one more explanation in an attempt to help you to envision the effect of this parameter. I will do this by describing an animated scene. I recommend that you actually create this scene and observe its behavior as you read my description.
A description of the world
Begin with a new world containing the ground, the light, the camera, and an ice skater. Align the viewpoint of all the objects to the viewpoint of the world. Then turn the camera to face north, move it to a position that is about twelve meters to the south of the center of the world, and move it up about one meter above the ground. At this point, the blue axis belonging to the camera will be parallel to the ground pointing due north across the center of the world and the center of the ground.
Turn the ice skater to face due east, and move her west by three meters. At this point, she will be on the left side of the scene as viewed by the camera, facing due east. Her blue axis will be pointing due east across the center of the world and the center of the ground.
Two different animation scenarios
We will consider two different animation scenarios. For the first scenario, the ice skater will simply glide six meters east, ending up on the right side of the scene, still facing east. On the second scenario, she will do the same thing, but in addition, she will turn a flip in the air as she traverses the middle two meters of the trip.
The first scenario
For the first scenario, the animation could consist of a single statement causing the ice skater to move forward for six meters. However, for reasons that will become more obvious later, we will write three statements, each one of which will cause her to move forward by two meters. To make the motion look smooth, we will use the style parameter to cause an abrupt transition between the three segments of motion.
A very important point
Although we could accomplish each segment of this motion by causing the ice skater to move FORWARD, simply accepting the default value for the asSeenBy parameter, we could also accomplish exactly the same thing by causing the ice skater to move RIGHT asSeenBy the camera. Optionally, we could accomplish the same thing by causing the ice skater to move LEFT asSeenBy the ground.
The easiest way to accomplish this motion would be to simply accept the default value of the asSeenBy parameter which is what we will do. This will cause the skater to move forward relative to herself, or more technically asSeenBy herself.
The second scenario
In the second scenario, we want the ice skater to turn a flip in the air during the second two-meter segment of the trip across the ice. (Now you will see why I broke the trip into three segments, each two meters in length.) We don't need to modify the behavior of the ice skater during the first and third segments, so we can leave that code alone and modify only the code that describes the behavior of the ice skater during the middle two-meter segment.
How to turn a flip in the air
Causing the skater to turn a flip in the air is a relatively simple thing to do. All we need to do is to cause the skater to turn (rotate) FORWARD around the middle part of her body and to keep moving forward at the same speed while rotating. Because we want the two actions to happen concurrently, we will need to enclose the code to rotate and the code to move forward within a doTogether block.
|
Simply add a turn Forward statement
Let's begin by placing the existing move statement for the second segment in a doTogether block and add a turn FORWARD statement to cause the skater to turn forward asSeenBy her skirt (which is one of the component objects that makes up the ice skater near the center of her body). This will cause the skater to rotate forward around the center of her body. (Note that this is another important use of the asSeenBy parameter.)
|
What's wrong with this picture?
When you cause an object to move forward asSeenBy itself, you cause it to move in the direction of the blue axis belonging to the object. Therefore, the existing statement that causes the skater to move forward for two meters during the middle segment of her trip causes the skater to move in the direction of the blue axis belonging to the skater.
How does the skater's blue axis behave?
What happens to the orientation of the skater's blue axis as the skater is rotating around the center of her body? If you could see the skater's blue axis while she is rotating, (see the sidebar regarding an Axes object) you would see that the blue axis also rotates much like the big hand on a clock. In fact, it starts out pointing east, makes a complete rotation pointing to each of the numbers on the face of an imaginary clock, and ends up pointing east again.
What happens to the skater's eastward motion?
Because the skater moves in the direction in which her blue axis is pointing, her eastward progress is stymied while she is rotating. In fact she moves down (toward the 6 on the face of the clock) a little, moves west a little, moves up a little, etc. When viewed as an animation, she actually appears to stop moving east while rotating around her skirt and then starts moving east again once the rotation is complete.
Newton would not be pleased
According to the laws of physics, we know that if she is moving forward when she begins her flip, she will continue to move forward as the flip progresses. We will need to do something to guarantee that she continues moving east regardless of the fact that her blue axis is rotating like the big hand on a clock.
And the solution is...
Fortunately, the solution to this problem is relatively simple. Rather than to cause the skater to move FORWARD asSeenBy herself during the middle two-meter segment of her trip, we can cause to the skater to either:
With the first option, she will continue to move in the direction of the red axis belonging to the camera. With the second option, she will continue to move in the opposite direction of the red axis belonging to the ground. Since neither of these axes will change their direction while she is doing her flip, her eastward progress won't be impeded by the fact that she is doing a flip.
More on the asSeenBy parameter later
We will see more interesting applications of the parameter named asSeenBy in conjunction with the discussions of the roll and turn methods later.
Other default parameters
Unless I made an error in compiling it, Table 1 shows all of the optional values for the two required parameters and the four default parameters belonging to the move method. The two required parameters and the four default parameters are shown in boldface. The various optional values for the different parameters are shown in regular typeface.
Table 1. Parameters and their options for the move method.
|
Note that other primitive methods may have fewer default parameters, more default parameters, or different default parameters than those shown for the move method in Table 1.
Wrap-up for the move method
Now you know how to use the method named move. You also know to use the duration, style, and asSeenBy parameters, which are common to many of the 20 primitive methods.
The next stop on the recommended study trail
You also learned a little about the turn method, but there is much more to learn about that method. The turn method and the roll method are very closely related. I recommend that you study the roll method next because it is a little simpler than the turn method.
Recommended study trail: Return to the explanation of the method named roll.
Brief description: A method to cause an object to either rotate around its red axis or its green axis, or to rotate around the red axis or the green axis belonging to another object.
|
The turn method and the roll method are very closely related. If you have studied the material on the roll method, you know this to be true because it is possible to call the roll method and get results normally considered to be the purview of the turn method. Similarly, as you will see in this explanation of the turn method, it is possible to call the turn method and get results normally considered to be the purview of the roll method.
I elected to discuss the roll method before discussing the turn method because the roll method is somewhat simpler than the turn method. At least, the turn method has fewer allowable values for its first required parameter.
Brief description of the turn method
As you learned in the discussion on the roll method, if you call the roll method on an object, and you don't specify some other object as the value for the default parameter named asSeenBy, the object will rotate around its own blue axis.
Similarly, if you call the turn method on an object and you don't specify some other object as the value for the default parameter named asSeenBy, the object will either rotate around its own green axis or rotate around its own red axis. The choice depends on the value that you pass as the first required parameter.
Required parameters
The turn method has two required parameters plus a variety of default parameters. The two required parameters are:
The allowable values for the first parameter are:
Specifying either of the first two parameter values given above will cause the object to rotate around its green axis (or the green axis belonging to another object). This is similar to turning a corner in an automobile.
Specifying either of the last two parameter values will cause the object to rotate around its own red axis (or the red axis belonging to another object). This is similar to an airplane flying along straight and level and then diving straight into the ground or climbing up toward outer space.
Allowable values for the amount parameter
You can specify any numeric value for the second required parameter named amount. This parameter specifies the amount of rotation to be executed. The value is given in revolutions or fractions thereof.
Three important aspects of the turn method
I will illustrate three important aspects of the turn method in this section:
The program named turn01
Let's get started writing (or downloading) the first program named turn01. I will explain things as we go along.
Create a new world, select the snow template, and save the world as turn01. Get a ToyPlane object from the Objects section of the Web Gallery (not the Local Gallery). Add the object to the world and rename it airplane.
Position is not critical
You can place the airplane anywhere in the world that you choose, because we will set its initial viewpoint with program code. Figure 8 shows an example of a raw world containing an airplane before the program starts running.
The red, green, and blue axes are visible
If you look carefully at Figure 8, you can see the blue axis protruding from the front of the airplane. You can also see the red axis protruding from the right wing, and the green axis sticking straight up from the cockpit.
The behavior of the turn method
As explained earlier, the default behavior of the turn method causes the object to rotate around its own red axis or its own green axis, depending on the value that you specify for the first required parameter.
Another option is to cause the object to rotate around the red or green axes belonging to another object. When the corresponding axes of the two objects are not parallel, the first object will rotate around the second object in a very complex way.
Description of the program
In this program, the airplane crosses the field of view of the camera moving from right to left. At first, the airplane flies level as shown in Figure 21. (This airplane object has a natural tilt when it is flying level.) Part of the way across the screen, the pilot pulls the control stick back causing the airplane to rotate BACKWARD around its red axis. This causes the airplane to climb. During the remainder of the trip across the screen, the airplane climbs as shown in Figure 22. (I will show you a much better way to do this later in conjunction with the method named moveAtSpeed. See Figure 50.)
Two screen shots of the running program
Figure 21 and Figure 22 show two screen shots taken while the program named turn01 was running.
Figure 21. Screen shot near the beginning of the program named turn01.

|
Figure 22. Screen shot near the end of the program named turn01.

|
Source code for the program named turn01
Listing 5 shows the source code for the program named turn01.
A relatively simple program
As you can see, this is a relatively simple program. Most of the code is used to initialize the viewpoints of various objects. You have seen lots of code like this before.
First call to the turn method
The first call to the turn method occurs in the section of code identified by the comment "Set viewpoint of the camera and the ground." As you can see, this method call causes the camera to rotate to the LEFT by one-half a revolution around one of its axes. Do you know which axis it will rotate around?
The green axis
The camera rotates around the green axis as a result of this method call. (This is part of the viewpoint initialization and not part of the actual animation that will be presented to the viewer.). The airplane will be flying from east to west, and the camera will be south of the airplane's path. This method call is necessary to cause the camera to face north so that it can see the airplane as it passes by.
Set viewpoint of the airplane
The next call to the turn method occurs in the block of code identified by the comment that reads "Set viewpoint of the airplane." This instruction to turn RIGHT causes the airplane to rotate around its green axis. The purpose of this method call is to turn the airplane to face the west. Then it will be moved backwards to the east side of the screen to get it ready to be animated.
Perform animation
The next and last call to the turn method in this program occurs in the block of code identified by the comment "Perform animation." Do you know which axis the airplane will rotate around as a result of this instruction to turn BACKWARD?
The red axis
If your answer was the red axis, you were correct. This method call causes the nose of the airplane to pitch upward, which in turn causes it to climb during the remainder of the trip across the screen.
Three sections of animation code
Note that this animation code is broken into three sections. The first section causes the airplane to move from right to left across the screen for a distance of one meter. This section of the trip occurs during a three-second interval and ends abruptly.
The second animation section comprises the code in the doTogether block, which causes the airplane to perform the following actions concurrently:
Note that both the turn and the move in this section begin and end abruptly and the move in the previous section ended abruptly. This causes the motion in the second section of code to fuse smoothly into the end of the motion for the first section. If those motions were caused to begin and end gently, there would be a noticeable pause at the interface between the two motions.
Once the turn has been completed, the airplane's blue axis is pointing up at an angle. The last section of animation code causes the airplane to move forward along the blue axis, which causes the airplane to appear to climb.
The program named turn02
This program illustrates the behavior of the turn method where one object rotates around the red axis belonging to another object and the two red axes are perpendicular to one another.
The airplane and the blimp
We will return to the scenario of the airplane and the blimp, which you have seen earlier. In this program, a small blimp is positioned directly beneath the initial position of the airplane. The airplane is facing due south, causing its red axis to point due west. The blimp is facing due east, causing its red axis to point due south.
Figure 12 shows the airplane and the blimp before they are moved into their initial viewpoints by the program code.
Convert a turn into a roll
To make a long story short, after initializing the viewpoints of the objects, the animation section of the program instructs the airplane to turn FORWARD around the red axis belonging to the blimp. However, if you use the source code in Listing 6 to write this program (or download it) and then play the world, you will see the motion more closely resembles a roll than a turn. The airplane flies forward along the blimp's red axis, rolling around that axis in a spiral fashion during the entire trip.
Screen shot near the end of the program named turn02
Figure 23 shows a screen shot of the airplane as it coming out of its last roll moving in a clockwise direction, getting ready to level out and fly over the camera.
Figure 23. Screen shot near the end of the program named turn02.

|
Source code for the program named turn02
The source code for the program named turn02 is shown in Listing 6.
This is also a relatively simple program, with most of the code being used to initialize the viewpoints of the various objects.
The initial viewpoints of the camera, the airplane, and the blimp
The initial viewpoint of the camera is at the center point of the world, facing due north, with an altitude of 20 meters.
The initial viewpoint of the airplane is ten meters north of the camera, facing due south with an altitude of 20.3 meters. Its red axis points to the west.
The initial viewpoint of the blimp is also ten meters north of the camera. The blimp's altitude is 20 meters, which is 0.3 meters below the airplane. The blimp is facing due east (see the call to the turn method in Listing 6) which causes the blimp's red axis to point due south (into the camera lens).
Skip down to the animation section
The call to the turn method in the animation section near the bottom of Listing 6 instructs the airplane to turn FORWARD for two revolutions in 15 seconds asSeenBy the blimp. In other words, this is an instruction for the airplane to rotate around the red axis belonging to the blimp.
Convert a turn to a roll
As you learned in an earlier discussion of the roll method, under certain circumstances, the roll method can turn a roll instruction into a turn. In this program, the motion of the airplane more closely resembles a roll than a turn. Thus, the circumstances of this program cause the turn method to produce a roll instead of a turn.
Why do I say that the behavior more closely resembles a roll than a turn? The airplane's nose doesn't pitch up or down in a direction that is perpendicular to the length of the wings, and the airplanes wing does not rotate around the airplane's green axis. Those are the characteristics of a turn. Rather, the airplane's left wing tilts downward and its right wing tilts upward, causing it to fly a spiral pattern around the blimp's red axis. This is what we would typically call a roll, not a turn. The airplane ends up flying directly over the camera at the end of the specified two revolutions.
The program named turn03
This is a long and rather complicated animation program that illustrates various aspects of the turn method. To set the stage, please take a look at Figure 24.
Figure 24. Setting the stage for the program named turn03.

|
|
As you might guess from Figure 24, this animation is a story about five penguins and a Zamboni® Ice Resurfacing Machine.
The program begins with three penguins standing in a line facing the front of a zamboni and two penguins standing on either side of the zamboni facing the other three penguins.
Description of the animation
To make a long story short, the zamboni starts moving toward the three penguins in the line. Only the middle penguin is in danger of being run over. The zamboni will fit between the other two penguins in the line. The middle penguin dives head first, burrowing into the ice (an obvious impossibility) and the zamboni passes above him without injury to life or limb.
Safe and sound
After the zamboni passes over the penguin, he emerges from the ice and stands back up. Shortly thereafter, all three of the penguins in the line turn to watch the back of the zamboni as it moves away from them.
A camera on a news helicopter
While all of this is happening, the camera is circling above the zamboni much in the fashion of a modern news camera mounted on a helicopter.
As you can tell from the description, there is quite a lot of action in this animation. Much of that action hinges on the use of the turn method.
Penguin diving for cover in the program named turn03
Figure 25 shows the middle penguin in the group of three penguins diving for cover in front of the zamboni. (Note the almost prone position of the middle penguin at this point in the animation.) The other two penguins in the group are far enough off to the side to be out of danger of being run over by the zamboni.
Figure 25. Penguin diving for cover in the program named turn03.

|
|
Note that the apparent orientation of the scene in Figure 25 is different from that in Figure 24. This is because the camera is mounted on a news helicopter, which is capturing the images from different viewpoints as the execution of the animation progresses.
In Figure 24, the two penguins were to the right of the line of three penguins in the camera's viewfinder. In Figure 25, the viewpoint of the camera has swung around to approximately on the other side of the scene. The two penguins are now to the left of the line of three penguins in the camera's viewfinder. Also, the zamboni was facing to the left in Figure 24 and it is facing to the right in Figure 25.
Penguin emerges from the ice
Figure 26 shows the penguin emerging unscathed from the ice after the zamboni has passed safely overhead. Once again, note the different viewpoint of the camera relative to the previous two figures. The penguin on one end of the line of three penguins is hidden behind the zamboni, and one of the penguins in the group of two penguins is almost completely out of range of the viewfinder on the left side.Figure 26. Penguin emerges from the ice in turn03.

|
And they all lived happily ever after
Figure 27 shows the three penguins back in their line, having turned to watch the runaway zamboni move away from them. The camera viewpoint in Figure 27 is very close to the camera viewpoint in Figure 24. Note, however, that the camera has made two complete revolutions around the zamboni by this point in the animation. Also note that the zamboni is once again facing to the left, and has moved almost to the left edge of the camera's viewfinder.
Figure 27. And they all lived happily ever after.

|
Source code for the program named turn03
The source code for the program named turn03 is shown in Listing 7. To write this program using the source code in Listing 7, you will need to create a new world containing a zamboni and five penguins with a snow template. You can also download the program.
Skip down to the animation section
There are several calls to the turn method in the early portions of the program that initialize the viewpoints of all the objects. You are already familiar with the use of the turn method for viewpoint initialization, so I will skip all the way down to the section of code identified by the comment "Perform animation." The first significant new use of the turn method occurs immediately thereafter.
Make the camera pointAt the zamboni
Note that the block of code immediately before the "Perform animation" comment calls the method named pointAt on the camera to cause the blue axis of the camera to point directly at the zamboni. (I explain the pointAt method in a different section of this document.) Therefore, when the animation code begins executing, the zamboni is in the center of the camera's viewfinder, as shown in Figure 24.
|
The structure of the animation code is a little complex in Listing 7. In particular, all of the animation code is contained in a doTogether block, which begins with an instruction to the camera to turn right, two revolutions in ten seconds, asSeenBy the zamboni. Therefore, rather than to rotate around its own green axis, the camera will rotate around the green axis belonging to the zamboni.
An analogy
Consider attaching your new battery-operated digital video camera to the end of a long pole, with the lens of the camera (the blue axis) pointing along the length of the pole. If you extend that pole directly in front of you, stand in one spot, and spin around, the camera will continue taking a video of you even though you are spinning. The items in the background will appear to be zooming by as the video progresses.
In this case, the rotational motion of the camera is matched to your rotational speed. As a practical matter, it will look like you are standing still and everything behind you is moving. That will be true even if you are standing on a moving sidewalk while you are spinning. You will continue to appear in the center of the viewfinder of the camera and will not appear to be spinning.
What if you don't spin with the camera?
Assume that you can come up with some sort of a mechanism that will cause the camera to circle around you on the same path without a requirement for you to spin. In that case, the video will make it appear that you are spinning and the items in the background will be moving also. Again, that will be true even if you are standing on a moving sidewalk and you cause the video camera to circle around you at the same rotational velocity, maintaining the same distance from you as you move. You will continue to appear in the center of the camera's viewfinder and you will appear to be spinning.
Similar to this animation
That is the case in this animation. The camera is circling the zamboni while the zamboni is moving forward. The zamboni is not spinning. However, the zamboni remains in the center of the viewfinder during the execution of the doTogether block in Listing 7 and appears to be spinning as you watch the animation.
The penguins and the horizon also appear to be spinning, but because the zamboni is moving while they are standing still, their orbits around the zamboni are not circular. For example, because the camera is tracking the forward motion of the zamboni, the two penguins that were originally standing beside the zamboni appear to be closer to the camera as they come into the foreground during each revolution.
Some actions must be performed in sequence
Continuing with the discussion of the animation code in Listing 7, even though the circular camera motion needs to occur concurrently with everything else in the animation, there are other actions that need to happen sequentially. For example, the penguin shouldn't be emerging from the ice at the same time that he is diving into the ice. Therefore, the doTogether block is subdivided into several sequential code blocks each of which is inside a doInOrder block.
Move the zamboni forward
The first block of sequentially executed code simply causes the zamboni to move forward by five meters over an interval of 2.5 seconds beginning gently and ending abruptly. The purpose of this statement is to move the zamboni closer to the three penguins that are standing in a line. The penguins don't do anything during this interval.
Make zamboni run over penguin
This is followed by a block of code identified by the comment that reads "Make zamboni run over penguin." This block contains three statements that are executed concurrently. The first statement causes the zamboni to move forward by 7.5 meters in 3.75 seconds, beginning and ending abruptly.
The second statement, which is executed concurrently with the first, causes the penguin to turn FORWARD by 0.25 revolutions, effectively causing him to lay face down on the ice. (See the position of the middle penguin in the group of three penguins in front of the zamboni in Figure 25.)
Rotate around the right foot
Note that this turn action causes the penguin to rotate around the red axis belonging to his right foot, (by virtue of the value of the parameter named asSeenBy) instead of rotating around the center point of the entire penguin.
|
Sometimes this can make a big difference, but in this case, it doesn't matter very much. This is because the red axis of the right foot is parallel to and very close to the red axis belonging to the entire penguin. (The center point of the penguin is between his feet at the level of the soles of his feet.) However, I wanted to illustrate that a turn action can not only be made relative to an axis belonging to a completely different object, it can also be made relative to one of the component objects that make up the object on which the method is called (a foot, a hand, or a head for instance).
Sink into the ice
The third statement in this doTogether block in Listing 7 causes the penguin to sink into the ice by 0.3 meters, effectively protecting his backside from the mechanism on the bottom of the zamboni that resurfaces the ice.
Penguin recovers, zamboni keeps going
The next block of code that is executed in sequence is identified by the comment that reads "Penguin recovers, zamboni keeps going."
|
This block of code also contains three statements that are executed concurrently. The first two statements essentially reverse the process described above. These statements cause the penguin to rise back up out of the ice and to stand up by calling the turn method with a value of BACKWARD for the first required parameter. Again, the turn is made relative to (asSeenBy) the penguin's right foot.
Keep that zamboni moving
The third statement in this doTogether block causes the zamboni to move forward by another 5 meters. At this point, the runaway zamboni runs out of fuel and stops.
All penguins turn to face the zamboni
As the zamboni reaches the end of its trip, the three penguins in the line all turn to face the back of the zamboni. (I explain the turnToFace method elsewhere in this document.) It is important to note that the camera is still circling the zamboni when this happens, and the zamboni is still in the center of the camera's viewfinder.
Pan the camera to the middle penguin
When the camera completes the two revolutions around the zamboni, one additional statement identified by the comment that reads "Make camera pan to penguinA" causes the camera to point to the middle penguin in the group of three penguins. This moves them to the center of the camera's viewfinder and causes the now-parked zamboni to move toward the left side of the viewfinder.
And they all lived happily ever after
The penguin was saved from destruction by a runaway zamboni, and they all lived happily ever after.
The next stop on the recommended study trail
The program discussed above calls both the pointAt method and the turnToFace method, which are explained elsewhere in this document. These two methods have similar behavior, but there are significant differences. I recommend that you study the method named turnToFace next.
Recommended study trail: Return to the discussion of the method named move.
Brief description: A method to cause an object to rotate around its blue axis, or around the blue axis of some other object as specified by the asSeenBy parameter.
Closely related methods
The roll method and the turn method are very closely related, but the roll method is the simpler of the two, so I will begin with it. One of the best ways that I have found to explain the roll method is to use an airplane as an example.
Three important aspects of the roll method
I will illustrate three important aspects of the roll method in this explanation:
The program named roll01
Go ahead and get started writing (or download) the program named roll01. I will explain things as we go along.
Create a new world. Select the snow template. Save the world as roll01. Get a ToyPlane object from the Objects section of the Web Gallery. Add it to the world and rename it airplane.
Position is not critical
You can place the airplane anywhere in the world that you choose, because we will set its initial viewpoint with program code. However, you should try to place it in such a way that you can see the red, green, and blue axes for the airplane when the program is not running. Figure 8 shows an example of my raw world before the program starts running.
Figure 8. Raw world for the program named roll01.
 |
The red, green, and blue axes are visible
If you look carefully at Figure 8, you can see the blue axis protruding from the front of the airplane. You can also see the red axis protruding from the right wing, and the green axis sticking straight up from the cockpit. Remember, blue for front, red for right, and green for top.
The behavior of the roll method
In a word, the default behavior of the roll method causes the object to rotate around its own blue axis. Another option is to cause the object to rotate around the blue axis belonging to another object.
When the blue axes of the two objects are not parallel, the first object still rotates around the second object, but in a very complex way. I can't explain the rules that govern that rotation. However, the three programs that we will develop in this explanation of the roll method will illustrate all three possibilities.
Required method parameters
The roll method requires two parameters:
The direction of rotation
To help you understand the meaning of the direction of rotation, if the airplane object rolls to the right around its own blue axis, the right wing will tilt downward and the left wing will tilt upward. (The simplicity of that explanation is why I like to use an airplane to illustrate the roll method, and some other methods as well.)
Default parameters
In addition to the required parameters, the roll method also has several default parameters including duration and style. Both of those default parameters will be used in this program.
Description of the program
When this program starts running, the airplane is quite a distance away from the camera, facing the camera when it first becomes visible.
The airplane flies in the direction of the camera rolling to the right around its own blue axis along the way.
Because the altitude of the airplane is slightly higher than the altitude of the camera, the airplane does not collide with the camera. Rather, the airplane would fly over the camera if I allowed the program to run that long. However, I caused the animation to stop just before the airplane completely passed over the camera so that I could get a screen shot of the airplane's tail section as it passed over the camera.
Some "stills"
About 100 years ago, I worked as an usher at a movie theatre. Whenever the movie that was showing was replaced by another movie, it was my job to change the letters on the marquee. It was also my job to replace the "still shots" of the movie in the glass cases at the front of the movie theatre so patrons could get a look at some of the scenes in the movie before purchasing a ticket. We called those photographs "stills."
Three "stills" from the animation
Figures 9 through 11 show screen shots taken at three different points during the running of the program. These three screen shots illustrate how the airplane is rolling around its blue axis and getting closer to the camera at the same time.
Figure 9. The roll01 program shortly after startup.
 |
Figure 10. The roll01 program about midway through the run.
 |
Figure 11. The roll01 program at the end of the run.
 |
Source code for roll01
Listing 2 shows the source code for the program named roll01. All of the code is in the main method.
Quite a lot of familiar code
If you followed the discussion of the code in the program named move01, in the description of the move method, much of the code in this program will be very familiar to you. Therefore, I will either skip over that code, or mention it only briefly.
|
Make the objects invisible while setting their initial viewpoints
Unlike the earlier code in the program named move01, this program makes all of the objects invisible before moving them around for the purpose of setting their initial viewpoints. This is accomplished by setting their isShowing property value to false using program code. The objects are all made visible later once the initialization of the viewpoints is complete and it is time for the animation to begin.
Initial viewpoint for the camera
In this program, the camera is allowed to remain at the center point of the world. It is rotated by 180 degrees so that it will be facing north. It is raised above the ground by two meters without changing its orientation.
Initial viewpoint for the airplane
The initial viewpoint for the airplane is 15 meters due north of the center of the world, facing south (facing the camera). The initial altitude of the airplane is 2.3 meters, which is slightly higher than the camera.
The airplane flies due south
When the animation is run, the airplane moves forward by 14 meters and stops slightly above and slightly to the north of the camera. Ten seconds are required for the airplane to complete the trip, which begins and ends abruptly.
|
During the first 9.8 seconds of the trip, the airplane rolls to the right, around its own blue axis, completing two revolutions during that period. The roll begins and ends gently, with the airplane leveling out at the end of 9.8 seconds. Motion stops at the end of 10 seconds with the airplane's tail section still being in view of the camera. (See Figure 11.)
Write (or download) the program and play the worldI highly recommend that you either write or download this program and play the world. This should give you a good feel for the default behavior of the roll method.
The program named roll02
This program illustrates the behavior of the roll method when the object rotates around the blue axis belonging to another object and the two blue axes are parallel. In this program, a small blimp is positioned directly beneath the initial position of the airplane, with both objects facing due south. Therefore, the blue axes of the two objects are parallel.
The airplane and the blimp
Figure 12 shows the airplane and the blimp before they are moved into their initial viewpoints by the program code.
Figure 12. The airplane and the blimp.
 |
You saw the red, green, and blue axes for the airplane earlier in Figure 8. You can see the red, green, and blue axes for the blimp in Figure 12.
Airplane, please make your move!
Once the initial viewpoints of the two objects are established and the animation begins, a message is sent to the airplane asking it to move forward 14 meters in 10 seconds, beginning and ending abruptly. The airplane is also asked to concurrently roll around the blue axis belonging to the blimp (asSeenBy the blimp), completing two revolutions in eight seconds, beginning and ending the roll gently.
Then fly straight and level
Because the rolls are completed in less time than the time required to complete the 14-meter trip, the airplane ends up flying straight and level at an altitude that is slightly higher than the camera.
Let's see the stills
Figures 13, 14 ,and 15 show screen shots at three points during the running of the program.
Figure 13. Program roll02 shortly after startup.

|
Figure 14. Program roll02 about midway through the run.

|
Figure 15. Program roll02 near the end of the run.

|
The small silver object in the background in Figures 13, 14, and 15 is the front end of the blimp. (The blimp is directly facing the camera at some distance north from the camera, so it appears to be round.) Although it can't be seen, there is an imaginary blue axis emerging from the front of the blimp that is pointed directly into the camera lens. That blue axis is the reference around which the airplane is requested to roll in the animation code.
Source code for the program named roll02
The source code for this program is shown in Listing 3.
By now, you should understand everything down through the block of code that sets the initial viewpoint of the airplane.
The initial viewpoint for the blimp
Also, given the comments in the code, you should have no difficulty understanding the code that sets the initial viewpoint for the blimp. (Note that once the initial viewpoint for the blimp is set, it doesn't change throughout the remainder of the program.)
I will point out, however, that the blimp is positioned directly below the initial position of the airplane, facing due south, at the same altitude as the camera, with its blue axis pointing directly into the lens of the camera. The blue axis for the blimp is parallel to the blue axis for the airplane, which passes above the camera at a distance of 0.3 meters above the camera.
The new code
The first and only code in Listing 3 that is really new to the program is the very last statement in Listing 3. This is the code that calls the roll method on the airplane. The thing that is new and different about this code, relative to the program named roll01, is the last parameter in the method call that reads:
asSeenBy = blimp
This is the parameter to the roll method that instructs the airplane to rotate around the blue axis that belongs to the blimp instead of rotating around the blue axis that belongs to the airplane (which is the default). As usual, this parameter is specified through the use of popup menus when the statement is constructed using the drag-and-drop programming paradigm of Alice.
Write (or download) the code and play the world
A few stills such as Figures 13, 14, and 15 can't possibly do justice to an animation such as this. Therefore, I strongly urge you to download the code, play the world, and observe the behavior of the roll method when the method is used to roll one object around the blue axis belonging to another object for the case where the two blue axes are parallel.
Experiment with the code
I also urge you to experiment with the code, making changes to the code and observing the result of those changes. For this program as well as for all other programs in this appendix, you may find it instructive to modify the code that sets the viewpoint for the camera so that you can watch the action from other viewpoints.
|
The motion of the airplane in this program is somewhat more complicated than the motion of the airplane in the programs named roll01 and roll02. This program illustrates the result of instructing the airplane to roll around the blue axis belonging to the blimp when the blue axis belonging to the blimp is not parallel to the blue axis belonging to the airplane. The sample program is written so that there will be an angle of 45 degrees between the directions of the two blue axes.
Initial viewpoints
As before, the position of the blimp is 0.3 meters below the initial position of the airplane. However, the airplane is pointing due south, while the blimp is pointing southeast.
The starting position for the airplane is 15 meters due north of the center point of the world. The viewpoint of the camera is 5 meters south of the center point of the world, facing due north. Thus, the starting point for the airplane is 20 meters due north of the camera.
The altitudes of the camera and the blimp are both 20 meters, and the starting altitude of the airplane is 0.3 meters higher at 20.3 meters. As you will see when you download and play the world, the loops flown by the airplane are larger than in the program named roll02, so it was necessary to increase the altitude to allow for larger loops. It was also necessary to increase the initial separation between the airplane and the camera to provide a wider field of view.
|
Figures 16 through 20 show five successive screen shots taken while the animation program named roll03 was running.
Loops are large and offset to the right
As you can see, the loops made by the airplane are quite large, and they are offset toward the right side of the screen (the blimp's blue axis passes by the camera fairly far to the right). In the end, however, the airplane settles down on a straight and level course that causes it to pass directly over the camera.
Figure 16. Early screen shot from program named roll03.

|
Figure 17. Screen shot from program named roll03.

|
Figure 18. Screen shot from program named roll03.

|
Figure 19. Screen shot from program named roll03.

|
Figure 20. Late screen shot from program named roll03.

|
Source code for the program named roll03
The source code for the program named roll03 is shown in Listing 4.
Highlight a few items
Hopefully, by this point, none of the code in Listing 4 should require an explanation for you to understand it. However, a few things are worth highlighting.
Write (or download) the code and play the world
Once again, a few stills such as Figures 16 through 20 can't do justice to this animation. I urge you to download the code, play the world, and observe the behavior of the roll method for the case where the method is used to roll one object around the blue axis belonging to another object when the blue axes of the two objects are not parallel.
Experiment with the code
I also urge you to experiment with the code, making changes to the code and observing the result of those changes. For example, if you cause the blimp to face east while the airplane is initially facing south, (cause the blue axes of the two objects to be perpendicular) you will see that the airplane simply flies vertical loops around the blimp, making no net forward progress until the specified number of revolutions has been completed. At that point, the airplane levels out and continues its trip toward the south.
A very significant and complex result
This is a very significant, complex, and powerful result. As you learned earlier, when the airplane rolls around its own blue axis, one wing tips down, the other tips up, and in effect the motion is a sideways motion.
Looks more like a pitch motion
However, if you cause the blue axes to be perpendicular and observe the motion very carefully, you will note that the airplane's wings don't tip at all. Rather, the nose of the plane tips. The airplane files vertical loops around the blimp with its wings remaining parallel to the blue axis belonging to the blimp and perpendicular to the blue axis belonging to the airplane.
Similar to a forward turn
You will learn when we study the turn method that this is one of the behaviors that we expect from the execution of the turn method. If you cause the airplane to turn FORWARD, the nose of the airplane tips down and the wings don't tip in either direction. If you cause the airplane to turn BACKWARD, the nose of the airplane tips up and the airplane climbs. Again, the wings don't tip in either direction. This is what we call pitch in the set of three types of rotational motion commonly referred to as yaw, pitch, and roll.
|
As it turns out, if you instruct an object to roll around the blue axis of another object, and the blue axes of the two objects are not parallel, the resulting motion is a combination of pitch and roll, (and possibly some yaw as well). For the extreme case where the two blue axes are perpendicular to one another, the roll method converts the motion into pitch alone, which is normally thought of being the purview of the turn method.
Turn the blimp by an additional ninety degrees
On the other hand, if you turn the blimp by an additional ninety degrees, causing the blimp to face north while the airplane is initially facing south, this causes the blue axes to once again become parallel, and the behavior is what you would expect for parallel blue axes.
More than you ever wanted to know
And that is probably more than you ever wanted to know about causing an object to roll around the blue axis belonging to another object when the two blue axes are not parallel.
Causing an airplane to fly loops
At least now you know of one way to write an animation that causes an airplane to fly loops. Just cause it to roll around the blue axis of an invisible object whose blue axis is perpendicular to the blue axis belonging to the airplane.
The next stop on the recommended study trail
From here, I recommend that you study the closely related method named turn.
Recommended study trail: Return to the section titled The say and think methods for an explanation of both methods.
Brief description: A method to cause the size of an object to change by multiplying its current size by a specified scale factor.
Absolute sizes are typically required
Just about every visual programming application that I have ever dealt with requires the programmer to deal with the sizes of the various physical objects in an absolute way (or at least a relative way).
For example, given a world containing an ice skater and a penguin, it usually wouldn't be acceptable for the penguin to be as large as the ice skater. In that case, it may be necessary for the programmer to cause the ice skater to be 1.5 meters tall and to cause the penguin to be 0.5 meters tall. (Alternatively, it may be sufficient for the penguin to be one-third the height of the ice skater without a requirement to set the absolute height of the ice skater.) I will deal with the situation involving the requirement for absolute sizes in this section.
|
Size properties
Many visual programming languages provide property variables for the objects with names such as height, width, depth, etc. This makes it easy to write methods that set the values of the properties. Setting the various property values for size typically causes the object to take on that size in the visual display.
Unfortunately, Alice doesn't provide size-related property variables for its objects. Therefore, a little extra effort is required to control the size of objects in Alice in an absolute sense.
Available resources for controlling the size of objects
Alice does provide the following functions for most, if not all of its objects:
Alice also provides a primitive method named resize for most, if not all of its objects.
The resize method can be used in conjunction with one or more of the functions listed above to set the size of an object in either absolute or relative terms.
A sample program named resize01
This program illustrates one approach to writing code to control the size of objects in an Alice world.
Create a new world, select the snow template, name the new world resize01, and add the following objects to the world:
Interactively call the setPointOfView method to align the viewpoints of the two objects listed above, plus the ground and the camera, to the viewpoint of the world.
Source code for program named resize01
Write (or download) and run the program shown in Listing 11 to set the height of the ice skater to 1.5 meters and to set the height of the penguin to 0.5 meters. The final screen output is shown in Figure 44.
Set initial viewpoints of objects
As is the case with most of my Alice programs, the program in Listing 11 begins by setting the initial viewpoints of the objects. (Note that all of the methods in this program are allowed to execute with a default duration value of one second so that you can watch them execute.)
Set height of iceSkater to 1.5 meters
The resize method has a single required parameter named amount plus the following six default parameters:
The required parameter named amount specifies a scale factor that is used to scale the size of the object on which the method is called from the current size to a new size. Consequently, to use this method to set the absolute size of an object, you must know its current size. I will get back to that later.
The resize method can be very complicated
As is the case with many of the primitive methods, the behavior of the resize method is relatively simple if you accept the default values for all of the default parameters. However, the behavior of the method can become quite complicated if you specify new values for some or all of the default parameters. For example, you can specify a new value for the howMuch parameter to change the size of the penguin's head without changing the size of the rest of his body.
This program accepts the default values for all of the default parameters. I recommend that you experiment with all of the allowable values for all of the default parameters to get a feel for how they impact the behavior of the resize method.
Getting the current size of an object
As indicated above, the required parameter named amount specifies a scale factor that is used to scale the size of the object from the current size to a new size. In order to use this method to set the absolute size of an object, you must know its current size.
Two statements to set the ice skater's height
The code that was used to set the height of the ice skater to 1.5 meters in Listing 11 was broken into two statements. Note, however, that this code could have been combined into a single, more cryptic statement if desired.
The first statement calls the getHeight function on the ice skater object to get the ice skater's current height. It uses that value to compute a scale factor that can be used to resize the ice skater object to cause that object to have a new height of 1.5 meters. That value is saved in a local variable named resizeFactor.
The second statement calls the resize method on the ice skater object, passing the value stored in the variable named resizeFactor as the value of the required parameter named amount.
When you download and run the world, you can see the resize method in operation as the ice skater shrinks to about half her original size near the end of the run.
Set height of penguin to 0.5 meters
The code in Listing 11 that sets the height of the penguin is essentially the same as the code that is used to set the height of the ice skater. However, it references the penguin instead of the ice skater.
Final screen output from program named resize01
You will see quite a lot of activity on the screen when you play this world. Most of that activity is produced by the code that sets the initial viewpoints of the objects. The heights of the ice skater and the penguin are set to the specified values near the end of the run, producing the final screen output shown in Figure 44.
Figure 44. Final screen output from program named resize01.
 |
The next stop on the recommended study trail
As mentioned earlier, as long as you accept the default values for the default parameters, the behavior of the resize method isn't very complicated. Because the method has only one required parameter, which is a simple numeric scale factor, the method is also fairly easy to use.
As long as we are still discussing easy methods during our trip down the recommended study trail, I recommend that you study the method named playSound next.
Recommended study trail: Return to the discussion of the method named standUp.
Brief description: Both the say method and the think method cause a comic-strip bubble containing text to appear above the object. The difference between the two methods is how the bubble is connected to the object. See Figures 42 and 43 for examples.
Two more simple methods
The say method and the think method are almost identical. That is why I elected to combine the explanations for both of the methods into this single section.
Both methods have one required parameter named what and the following default parameters:
Before getting down into the weeds with the explanation, I'm going to show you two screen shots that should make this method almost self-explanatory. The first screen shot shows the result of calling the say method on a penguin. The second screen shot shows the result of calling the think method on a different penguin.
The behavior of the say method
The screen shot that is contained in Figure 42 shows the result of calling the say method on the penguin on the left and passing the string contained in the bubble as the value of the required parameter named what.
Figure 42. Execution of the say method in program say01.
 |
Figure 42 also shows the result of specifying the last four default parameter values in the above list with the values given in the bubble.
The behavior of the think method
Figure 43 shows the result of calling the think method on the penguin on the right and accepting the default values for the last four default parameters in the above list.
Figure 43. Execution of the think method in program say01.
 |
The only real difference between the two methods is the artwork that connects
the bubble with the object that is saying or thinking the text
shown in the bubble. Those differences in artwork are shown in
Figures 42 and 43. Both methods have the same default parameters
with the same default values.
The fontName parameter
As it turns out, there is only one choice for the fontName parameter, which is the last parameter in the above list. That single choice is Arial, so that default parameter seems not to have been completed in Alice 2.0. You might as well accept the default for this parameter.
Source code for the program named say01
The source code for the program named say01 is shown in Listing 10. The only code in Listing 10 that hasn't been explained in earlier discussions is the pair of statements that call the say method and the think methods at the end of the program. Even this code is straightforward. If you have been studying the programs along the recommended study trail through this appendix, you shouldn't have any difficulty understanding this code by now.
The next stop on the recommended study trail
Continuing with the examination of relatively easy primitive methods, I recommend that you study the method named resize next.
See the section titled The say and think methods for an explanation of both methods.
Recommended study trail: Return to the discussion of the method named resize.
Brief description: A method to cause the contents of a sound file to be emitted from the computer's audio speakers.
Alice can play sound files
Although the method named say doesn't cause actual sound to be emitted from the computer's audio speakers, there is a method named playSound that can play a sound file and cause the contents of the file to be emitted from the computer's audio speakers.
Available sound files
Alice version 2.0 contains sound files with the following names:
|
Import existing sound files and record new ones
In addition, Alice allows you to import existing sound files and to record new sound files.
Required and default parameters
The playSound method has one required parameter and four default parameters. The required parameter is named sound and its value must be the name of the sound file that is to be played.
The four default parameters are:
I will briefly discuss the default parameters shortly, but the names of the default parameters are relatively self-explanatory.
A fairly simple method
This is a fairly simple method to understand and to use. This is true even when the program changes the values of some or all of the default parameters, which is an unusual circumstance. (Often, changing the values of some of the default parameters causes the behavior of Alice primitive methods to become much more complicated.)
Brief description of the default parameters
The duration parameter can be used to limit the length of the time that the sound is played (by chopping off the end of the sound). However, it can't be used to extend the time beyond the normal time required to play the sound file at its normal speed.
The marker properties have default values based on the start and the end of the sound file. The sound file must contain some sort of markers for these two properties to have other allowable values.
The volumeLevel property has a numeric default value of 1. Other values can be specified to cause the sound output to be either louder or softer.
Maybe simplest of all primitive methods
Given all of the above, assuming that you will be using one of the sound files that are already contained in Alice 2.0, this may well be the simplest primitive method in Alice. (At least you don't have to worry about the effect of a property named asSeenBy, which is a complicating factor for most of the other primitive methods.)
Demonstrate the playSound method
You can demonstrate the playSound method by doing the following:
That's all there is to it. If the audio system on your computer is working properly, you should hear the sound of a chicken clucking.
The next stop on the recommended study trail
I recommend that you study the method named orientTo next.
Recommended study trail: Return to the discussion of the method named orientTo.
Brief description: By default, this method causes the position of an object to change so that its center point coincides with the center point of another object. The method can also be used to change the position of an object so that its center point coincides with an arbitrary point in 3D space specified by a position vector. The orientation of the object is not changed in either case.
One new topic
If you have been studying the material on the recommended study trail up to this point, you should find the moveTo method relatively easy to understand and easy to use. However, I will introduce one new topic in this discussion of the moveTo method. That new topic is vectors.
|
What does the moveTo method do?
With the moveTo method, you can cause an object to take either of two actions:
Parameters
The moveTo method has one required parameter and the following three default parameters:
The allowable values for the required parameter are any object in the world.
You are already familiar with the first two default parameters. The allowable value of the third default parameter is a 3D vector that specifies a point in 3D space relative to the center point of the object specified as the required parameter. If the world is specified as the required parameter, this vector specifies the position of a point in 3D space relative to the center of the world.
Two demonstration programs
I will present and explain two demonstration programs in this section. The first program, which is named moveTo01, demonstrates moving an object through 3D space to cause its center point to coincide with the center point of another object.
The second program, which is named moveTo02, demonstrates moving an object through space to a point that is specified by a vector relative to the center of the world.
The program named moveTo01
Two screen shots from the program named moveTo01 are shown in Figures 47 and 48. Figure 47 shows a partially transparent penguin object, (with visible axes attached), being moved from a position in the upper right of the screen to cause its position to coincide with the position of a magician wand object (with visible axes attached) at the center of the world.
Figure 47. Penguin in transient in program named moveTo01.
 |
Visible axes were attached
I attached visible axes to each object in Figure 47 to demonstrate that the orientations of the objects are not modified by the moveTo method. Only the position of one of the objects is modified.
Penguin is partially transparent
I also made the penguin partially transparent so that you can see the green axis belonging to the penguin protruding up through the penguin's body and sticking out the top of its head.
Final resting place for the penguin
Figure 48 shows the final resting place of the penguin object after the moveTo method was used to cause its position to coincide with the position of the magician wand object at the center of the world.
Figure 48. Penguin after being moved in program named moveTo01.
 |
|
The moveTo and setPointOfView methods
As mentioned earlier, calling the moveTo method on an object and passing another object as the required parameter will, by default, cause the first object to be repositioned so that the center points of the two objects coincide. However, the orientations of the objects will not be changed, as demonstrated by the fact that the axes of the two objects do not overlay one another in Figure 48.
Source code for the program named moveTo01
Listing 13 shows the source code for the program named moveTo01.
Move the penguin
You are already familiar with most of the code in this program, so I will skip all the way down to the last statement in the program. This statement calls the moveTo method on the penguin, instructing it to reposition itself so as to cause its center point to coincide with the center point of the magician wand object. I set the duration to five seconds to give me sufficient time to pause the action and grab a screen shot of the penguin in transient as shown in Figure 47. When used with this default behavior, the method is easy to understand and easy to use.
The program named moveTo02
The optional behavior of the moveTo method demonstrated by the program named moveTo02 is a little more difficult to understand, particularly if you are not familiar with the concept of representing points in 3D space as three-dimensional vectors.
In addition, I discovered what appears to be a bug in the Alice development environment that complicates matters even further.
What is a vector?
In Java, which is the underlying language in which Alice was written, a Vector object is an object of a class that, among other things, can be used to contain a group of references to other objects, making it possible to store and retrieve those objects using a positive numeric index.
In 3D graphics, a vector is typically an entity that is defined by three real numbers that can specify a point in 3D space. (Alice appears to refer to a point as a position.) Vectors are also used to specify distances and directions in 3D space. In short, a vector can be used to represent anything in 3D space that can be represented by three real numbers.
In Alice, a vector appears to be an object that can be used to contain three real number values. A vector object can be used to represent a position in Alice's 3D space, where the position is specified by three distances from a given reference point. If that reference is the center point of the world, the three values can be thought of as representing the absolute coordinate values of a point.
The moveTo method supports vectors (sort of)
As you will see when we examine the source code for the program named moveTo02, one of the optional behaviors of the moveTo method is to cause an object to reposition itself to a new position specified by the three values stored in a vector object.
Special ways to specify the three values
Because a vector object contains three independent values, a special capability is provided to make it possible to specify the three values independently of one another.
When you create a variable of type Position, (which is misspelled as Posistion on the Alice program edit screen, and whose value is a vector) and you drag the variable into your code, you are given several options for setting the values stored in the vector. These options include the opportunity to call any or all of the following three methods, passing the numeric value as a parameter to the method:
A possible bug in Alice
I found that I was able to successfully call these methods to specify the three values to be stored in the vector so long as I passed literal constant values as parameters. However, whenever I passed the name of another variable of type number as a parameter, the statement was simply ignored. Either I wasn't doing it correctly, or this is a bug in Alice.
Destroys an important connection to other programming scenarios
If it is a bug, it greatly reduces the usefulness of the vector option of the moveTo method. This is very significant problem. This option provides the capability of writing Alice 3D graphics programs in much the same way that they are written using other 3D programming languages that typically deal with position and direction vectors instead of forward, backward, up, down, etc.
Why no screen shots?
I didn't provide screen shots of this program because there isn't very much to show. When the program runs, it simply moves a penguin twice in succession to new positions based on the values of a vector. The significant thing about the program is that it uses position vectors and not what it does with those position vectors.
Source code for the program named moveTo02
The source code for this program is shown in Listing 14.
|
Declare a variable of type Position
This program declares a local variable of type Position (misspelled by Alice as Posistion) named myVector.
Setting the values in myVector
About two-thirds of the way down, the three methods listed above are called on myVector to set the values of two of its three components to 0.5 and to set the value of the third component to -0.5.
Tell the penguin to move
Then the program calls the moveTo method on the penguin object to cause it to reposition itself such that its center point will be aligned to the point in 3D space given by the three coordinate values stored in the vector object.
A clarification
In reality, these three values should be thought of as distances rather than as absolute coordinates. They are used to compute a set of three coordinate values for a point in space where the distances from that point to the center point of the object passed as the first parameter to the moveTo method match the three values contained in the vector object. (It is probably more correct to say that the distances from the point in space to the center point of the object match the negative of the three values stored in the vector object. It all depends on how you construct the sentence.)
For the special case of the world
For the special case used here, where the specified object is the world, whose center point is located at the origin of the world, the three values contained in the vector represent absolute coordinate values. Otherwise, they represent coordinate values relative to the center point of the specified object.
Watching the penguin move
The execution of this statement causes the penguin to move from its initial position to a new position that is up and to the left of the initial position on the screen.
Modify the vector and move the penguin
Then the code in Listing 14 calls the setDistanceRight method on myVector to change one of the values stored in the vector from 0.5 to -1. Once again, the moveTo method is called on the penguin to cause the penguin to reposition itself so as to coincide with the position specified by the three values now stored in the vector. This causes the penguin to move horizontally across the screen from left to right.
The next stop on the recommended study trail
Now that you know all about the primitive method named moveTo, I recommend that you study the method named moveToward next.
Recommended study trail: Return to the discussion of the method named moveTo.
Brief description: A method to cause an object to move a specified distance toward another object along an imaginary line that connects the center points of the two objects, without changing the orientation of either object. Also supports the asSeenBy parameter, which can complicate the behavior of the method.
Description of the method
By this point along the recommended study trail, you should find the moveToward method easy to understand and easy to use. The method has the following required parameters:
Movement along any straight line
It appears that the object will move along a straight line that intersects the center points of the two objects. The orientation of the moving object is not changed. Only the position of the object is changed. Depending on the relative positions of the two objects, this could be any straight line anywhere in 3D space.
Default parameters
In addition to the required parameters, the method has the following default parameters, all of which are familiar to you by now:
The program named moveToward01
This program contains a penguin and a magician wand. The penguin iteratively moves toward the magician wand, moving half the remaining distance during each iteration. At the end of each move, the penguin turns its head to look at the audience. I didn't show you any screen shots because they would be pretty boring, but the program does illustrate the use of the moveToward method.
Source code for the program named moveToward01
The source code for this program is shown in Listing 15.
Set initial viewpoints
The code begins by setting the initial viewpoints for all the objects. This code should all be familiar to you by now.
Animate the penguin
Skipping down to the code that is identified by the comment that begins with "Animate the penguin," the code uses a while loop to control the iterative behavior of the program.
The conditional clause
The conditional clause in the loop is based on the distance from the center point of the penguin to the center point of the magician wand. The program continues to loop while the distance between the penguin and the magician wand is greater than the depth of the penguin object (the depth of the bounding box for the penguin). Once that limit is reached, iterations cease, preventing the penguin from overrunning the magician wand.
Move one-half the distance during each iteration
The code inside the while loop causes the penguin to move half the distance to the magician wand during each iteration. Just to make things a little more interesting, the penguin turns its head to look at the audience at the end of each iteration.
The next stop on the recommended study trail
You can check the moveToward method off the list of methods that you need to study. I recommend that you study the method named moveAwayFrom next.
Recommended study trail: Return to the discussion of the method named moveToward.
Brief description: A method to cause an object to move a specified distance away from another object along an imaginary line that connects the center points of the two objects, without changing the orientation of either object. The behavior of this method is the reverse of the behavior of the moveToward method. Once again, the behavior can be made more complicated through use of the asSeenBy parameter.
Description of the method
Just as with the method named moveToward, by this point along the recommended study trail, you should find the moveAwayFrom method easy to understand and easy to use. This behavior of this method is just the reverse of the behavior of the method named moveToward that I explained earlier on the recommended study trail.
Required parameters
The method has the following required parameters:
|
What will be the direction of the movement?
Without doing some very complicated 3D math, it can be difficult to predict exactly which direction the object is going to move. It appears that the object always moves along a line that intersects the center points of the two objects, provided that the center points of the two objects don't coincide. Depending on the relative positions of the center points of the two objects, this could result in movement along any straight line in 3D space.
Default parameters
In addition to the required parameters, the method has the following default parameters, all of which are familiar to you by now:
The program named moveAwayFrom01
This program contains a penguin and a magician wand. The penguin iteratively moves away from the magician wand, moving half the distance during each iteration. At the end of each move, the penguin turns its head to the left. Iterations continue until such time as the size of the next move would be less than one-half of the penguin's depth.
I didn't show you any screen shots of this program because screen shots would be pretty boring, but the program does illustrate the use of the moveAwayFrom method.
Source code for the program named moveAwayFrom01
The source code for this program is shown in Listing 16. Given your background at this point, none of the code in Listing 16 should require an explanation in order for you to understand it.
The next stop on the recommended study trail
Well, you are on the home stretch. If you have been following my recommended study trail, you have completed sixteen of the twenty primitive methods. What's more, three of the remaining four primitive methods are very similar to one another. I recommend that you study the method named moveAtSpeed next.
Recommended study trail: Return to the discussion of the method named playSound.
Brief description: Causes the three axes of an object to become parallel with the corresponding axes belonging to another object, without changing the position of either object.
Description of the orientTo method?
In a nutshell, when you call the orientTo method on one object, specifying another object as a parameter, the first object will be rotated such that all three axes of the first object point in the same directions as the corresponding axes of the second object. Neither object has its position in 3D space modified. Thus, the orientTo method impacts only the directional orientation of the object's viewpoint.
Parameters
The orientTo method has one required parameter and the following three default parameters:
The allowable values for the required parameter are all objects belonging to the world.
You are already familiar with the first two default parameters listed above.
What is a quaternion?
If you already know about the quaternion, you are probably in the wrong course. In that case, you should probably be in an advanced 3D graphics programming course instead of a course in programming fundamentals.
Fortunately, you can do a lot of interesting and useful things with Alice without any requirement to know about or to use a quaternion. To back this up, I recently visited a local bookstore and examined the alphabetical index of six respectable Alice programming textbooks. Not one of the six listed quaternion in the alphabetical index.
Demonstrating the orientTo method
The program named orientTo01 demonstrates the use of the orientTo method to cause one object to be oriented the same as another object. Figure 45 shows a screen shot of the program output at a point where the penguin on the left has assumed a specific orientation as indicated by the arrows (more on these arrows later) but the penguin on the right hasn't yet been oriented to match the orientation of the penguin on the left.
Figure 45. Non-oriented penguins in program orientTo01.
 |
The result of calling orientTo on the rightmost penguin
Figure 46 shows the result of calling the orientTo method on the penguin on the right instructing it to assume the same orientation as the penguin on the left.
Figure 46. Oriented penguins in program orientTo01.
 |
As you can see, the axes belonging to the rightmost penguin point in the same directions as the axes belonging to the penguin on the left, indicating that both penguins now have the same orientation.
What are those arrows, anyway?
This is the first time that I have used the arrows shown in Figure 46 in a demonstration program on this recommended study trail. These arrows make it possible for you to observe the axes belonging to an object during the animation of that object.
The Shapes section of the Local Gallery contains a class named Axes. The visual manifestation of an object of that class is a set of three orthogonal axes or arrows as shown by the arrows connected to each penguin's upper beak in Figures 45 and 46.
When you are working in the scene edit mode and you select an object, the three axes belonging to that object become visible as shown in Figure 3. However, those axes aren't visible when the program is running.
Sometimes it is useful to be able to display the axes for an object (for test purposes) when the program is running. As shown in Figures 45 and 46, this can be accomplished by creating an object of the Axes class and attaching it to the object of interest.
Source code for the program named orientTo01
You will see how to connect the Axes object to an object of interest in Listing 12, which shows the source code for the program named orientTo01.
Setup code
Listing 12 begins by changing the background color from blue to orange so that the blue axis will show. Then it makes the ground invisible to get it out of the picture.
After that Listing 12 sets the initial viewpoints for all the objects and separates the two penguins to put some space between them.
Attaching axes objects to penguins
The next step in Listing 12 is to attach the two objects of type Axes to the upper beaks of the two penguins. The viewpoint of each Axes object is first aligned with the viewpoint of the corresponding penguin's upperBeak object. This guarantees that the arrows in the Axes objects will point in the same directions as the real axes belonging to the penguin's upper beaks. After that, the vehicle property of each Axes object is set to the corresponding penguin's upper beak. As a result of that, whenever the penguin's upper beak moves, the arrows go along for the ride.
Animate the penguins
The last step in Listing 12 is to animate the penguins so as to accomplish the objective that the program was designed to demonstrate. The penguin on the left is rotated into the viewpoint shown in Figure 45 by calling the roll method on the penguin and then calling the turn method on the penguin. (A time delay was inserted at this point to give me time to pause the animation output and grab a screen shot for use in Figure 45.)
Then the orientTo method was called on the rightmost penguin to cause it to orient itself in such a way as to match the orientation of the penguin on the left, producing the screen output shown in Figure 46.
The next stop on the recommended study trail
I recommend that you study the moveTo method next.
See the section titled The pointAt and turnToFace methods for an explanation of the turnToFace method in addition to the pointAt method.
Recommended study trail: Return to the discussion of the method named turn.
Brief description: The turnToFace method causes an object to rotate around its green axis, causing its blue axis to point in the direction of another object. The pointAt method causes an object to rotate around all three of its axes, if necessary, to cause its blue axis to point at the center point of another object. Complex behavior can result if the value of the asSeenBy parameter is set to any object other than the object on which the method is called.
A pair of very similar methods
Because of the similarity between the two methods, this section will explain both the pointAt method and the turnToFace method. The explanation will highlight the similarities between the two methods and the significant differences between the two as well.
Another airplane scenario
It is interesting how often the animation of an airplane provides a good scenario for explaining an Alice primitive method. Perhaps this is because most of us are familiar with the behavior of an airplane. An airplane has distinct parts, which most of us recognize by name (nose, tail, wings, cockpit, etc.). In addition, most of us are generally aware of how an airplane moves in 3D space, so the concept of an airplane in 3D space is familiar territory.
An anti-aircraft gunner
In this explanation of the pointAt method and the turnToFace method, you will be a World War II anti-aircraft gunner trying to shoot down an incoming, low-flying enemy airplane. The enemy airplane comes out of the north on a heading that will take it above your head slightly to your right (east). All of the while, it is rolling to the right around its own blue axis to cause itself to be a difficult target to hit.
A sample screen shot
See Figure 28, for sample screen shot of one of the programs that I will explain in this section. This program, named pointAt01, is implemented using the pointAt method. Later, I will show you similar results for a program that is implemented using the turnToFace method.
Figure 28. Early screenshot of the program named pointAt01.

|
You have the enemy plane in your sights
In Figure 28, the enemy airplane is approaching from the north on a heading that will cause it to pass overhead slightly to your right. You have the circular sight on your anti-aircraft gun firmly locked onto the incoming enemy airplane and you are ready to shoot it out of the sky.
You have run out of ammunition
Unfortunately, you run out of ammunition and all you can do is to watch as the enemy airplane passes overhead slightly to your east. (As you will learn later in this section, tracking the airplane like this is possible using the pointAt method, but is not possible using the turnToFace method except in rare cases.)
Airplane is in center of camera's viewfinder
The main purpose of the method named pointAt is to cause the blue axis belong to one object to point directly to the center point of another object.
Note that in Figure 28, the target airplane is in the center of the camera's viewfinder. This will continue to be the case throughout the program, demonstrating that the camera can execute yaw, pitch, and roll, as needed to keep the blue axis of the camera pointed directly at the center point of the target.
Airplane passing overhead
The airplane is passing overhead slightly to your east in Figure 29. Note that the center of the airplane is still in the center of the camera's viewfinder and the targeting circle on your anti-aircraft gun is still locked on the center of the airplane.
Camera has executed yaw, pitch, and roll
To reach this point in the animation, the camera has executed a RIGHT turn (yaw) toward the east to follow the airplane as it passes by. It has also executed a BACKWARD turn (pitch) to keep its blue axis pointing at the center of the airplane that is now substantially overhead. (Note how the horizon has dropped to near the bottom of the viewfinder.) The fact that the horizon is no longer level indicates that the camera has also executed a small amount of roll to the right.
Figure 29. Airplane passing overhead in program named pointAt01.

|
Airplane has passed overhead
Figure 30 shown a screen shot of the airplane after it has already passed overhead. The camera is still locked on the center of the airplane, and the center of the airplane is still in the center of the camera's viewfinder.
Figure 30. Airplane has passed overhead in program named pointAt01.

|
Airplane flies away
Finally, Figure 31 shows the airplane as it safely flies away on a course that is a few degrees east of due south. At this point, the camera has swung all the away around and it is now facing a few degrees east of south. It has also leveled off some because the horizon is rising. The airplane is still in the center of the viewfinder, meaning that the camera is still firmly locked on the center of the airplane.
Figure 31. Airplane flies away in program named pointAt01.

|
The source code for the program named pointAt01
The source code for the program named pointAt01 is shown in Listing 8.
Write (or download) and run the program
To write (or download) and run this program according to the source code in Listing 8, you will need to create a new world using a snow template. Get a ToyPlane object from the Objects section of the Web Gallery (not the Local Gallery). Add the object to the world and rename it airplane.
Get a Torus object from the Shapes section of the Local Gallery and add it to the new world.
Much of the code in Listing 8 should already be familiar to you and should not require a detailed explanation at this point.
Set viewpoint of the camera
The code in the block identified by the comment "Set viewpoint of the camera and the ground" places the camera at the center of the world facing northeast. Because the airplane will come in from the north, it will be necessary for the camera to turn to the left to locate and lock in on the target when the animation starts running.
The camera is at a height of two meters above the ground. The low-flying airplane is at an altitude of 2.3 meters, only slightly higher than the camera.
Set viewpoint of torus
The torus is used to form the gun sight. It is placed in front of the camera lens and attached to the camera by the code in the section identified by the comment "Set viewpoint of torus. Place in front of camera lens."
Most of this code should already be familiar to you. However, you may not be familiar with the vehicle property. When the vehicle property of one object is set to another object, the first object becomes attached to the second object and will ride along with it wherever it goes. In this case, the torus is attached to the camera, slightly in front of the camera lens. This produces the black circular gun sight object that you see in Figures 28 through 31. Note, however, that the opacity property of the torus is set to only 40% causing it to be partially transparent and to appear to be gray.
Set viewpoint of the airplane
The initial viewpoint of the airplane is 15 meters north of the camera and 0.3 meters higher than the camera with a heading that is four degrees east of south. By flying a straight and level course, the airplane will pass slightly above and slightly to the east (right) of the camera.
|
The code in the doTogether block in the section identified by the comment "Begin animation" in Listing 8 animates the airplane, the camera, and the torus.
The most important statement and the only thing that is new in this code is the call to the method named pointAt.
The airplane starts at a position that is 15 meters north of the camera and moves to a position that is 15 meters south of the camera, thus traveling 30 meters during an interval of 30 seconds.
The call to the pointAt method
The call to the pointAt method instructs the camera to cause its blue axis to point at the center point of the airplane during the entire 30 second interval. As mentioned earlier, the camera does not initially face the airplane. Rather, it faces the northeast 0.3 meters below the altitude of the airplane.
|
Therefore, when the animation begins, the camera turns left and tilts slightly upward to point its blue axis at the center of the airplane.
Once locked, it stays locked
Once the camera locks onto the target, the camera continues to execute the turns and rolls necessary to keep its blue axis pointed at the center of the airplane. The fact that the blue axis of the camera continues to point at the center of the airplane is evidenced by the fact that the airplane moves to the center of the camera's viewfinder shortly after the program starts and remains there throughout the remainder of the program.
The program named turnToFace01
This program is designed to illustrate the behavior of the method named turnToFace. This program is identical to the program named pointAt01, except that the call to the turnToFace method in the animation section of the code is enabled and the call to the pointAt method is disabled. Therefore, I won't consume additional space in this appendix by presenting the source code for the program. Just refer to Listing 8 and make the mental change described above.
Major difference between the two methods
The major difference between the pointAt method and the turnToFace method is the number of degrees of freedom that each method can use to lock on and to remain locked on a target. As you saw earlier, the pointAt method can execute yaw, pitch, and roll to achieve the goal of causing the object's blue axis to point directly at the center of the target object.
The turnToFace method can only execute yaw
On the other hand, this program indicates that the turnToFace method can only execute yaw to achieve its goal. It appears that it can neither pitch nor roll in that process.
|
Therefore, unless the object and its target are at the same elevation above the plane described by the red and blue axes, the turnToFace method can never point its blue axis directly at the center of the target object. It can only point its blue axis in the direction of the target object.
Won't necessarily maintain lock
Even if the object and its target are at the same elevation and a lock is achieved (pointing the blue axis directly at the target object), it cannot be maintained by the turnToFace method if the relative elevation between the two objects changes.
A defective anti-aircraft gun
It is as though your anti-aircraft gun in this program is constrained to swivel in a horizontal plane, but cannot tilt up or down, and cannot roll from side to side. Such an anti-aircraft gun would be very good for shooting a lot of holes in buildings in the neighborhood, but it wouldn't be very useful for shooting down airplanes as they fly overhead.
Some stills from the program
Figures 32 through 35 show screen shots taken from the program named turnToFace01 at approximately the same points in the running program as the screen shots shown in Figures 28 through 31.
Figure 32. Early screenshot of the program named turnToFace01.
 |
If you compare Figure 32 with Figure 28, you will see that although the method named turnToFace was successful in causing the camera to swing to the left to line up with the general direction of the target, it was unable to tilt the camera upward to place the targeting sight directly on the target.
Airplane passing overhead
Figure 33. Airplane passing overhead in program turnToFace01.
 |
Similarly, if you compare Figure 33 with Figure 29, you will see that because the target airplane is almost overhead, it well out of the range of the targeting sight. The turnToFace method cannot pitch the gun barrel up in order to put the targeting circle on the center of the airplane.
Targeting circle is in the center of the viewfinder
While the targeting circle is in the center of the viewfinder, unlike the case shown using the pointAt method in Figure 29, the airplane is well out of the vertical range of this anti-aircraft gun. Even if you had ammunition available, it wouldn't do you any good. You wouldn't be able to use this anti-aircraft gun to shoot the enemy airplane.
Figure 34. Airplane has passed overhead in program turnToFace01.
 |
Airplane has passed overhead
The situation in Figure 34 is similar to that shown in Figure 33. The target airplane has already passed overhead and is safely speeding off in a southerly direction, still well out of the vertical range of this anti-aircraft gun.
Figure 35. Airplane flies away in program named turnToFace01.
 |
Finally, in Figure 35, the enemy airplane has completely escaped. Within just a few seconds it will be out of the horizontal range of this anti-aircraft gun.
Summary of the difference between the methods
The method named pointAt can execute yaw, pitch, or roll to cause its blue axis to point directly at the center point of the target object.
The turnToFace method is constrained to use yaw only to cause its blue axis to point in the direction of the target object.
|
The asSeenBy parameter value
Note that in this program, the parameter named asSeenBy was set to the camera when the turnToFace method was called. Similarly, in the program named pointAt01, the parameter named asSeenBy was set to the camera when the pointAt method was called.
In both cases, setting this parameter to a different value (such as the default <none> for example) will result in radically different results.
The next stop on the recommended study trail
The two programs discussed in this section illustrate the similarities of the pointAt method and the turnToFace method. The programs also illustrate the significant differences between the two methods.
I recommend that you study the method named constrainToPointAt next.
Brief description: A method to cause the viewpoint of one object to be aligned with the viewpoint of another object.
Call the method to align two object's viewpoints
You can call the setPointOfView method on an object to cause that object's viewpoint to be aligned with the viewpoint of another object that you specify as a parameter.
I often begin my programs by aligning the viewpoints of all objects (including the camera) to the viewpoint of the world. That way, I know the viewpoint of every object when the program starts running. If need be I can keep track of every change in viewpoint that occurs for every object during the running of the program. Using this approach, the program can always know the viewpoint of every object. This can be very useful, for preventing unwanted collisions, for example.
Precautions to observe
If you elect to write code at the beginning of your programs to align the viewpoints of your objects with the viewpoint of the world, you should observe at least two precautions:
No need to write a program in this case
It is easy to demonstrate the behavior of the setPointOfView method without the requirement to write a program. You can manually observe the behavior of the method by doing the following:
The next stop on the recommended study trail
Now that you understand the setPointOfView method, which we will use to align all of our objects with the world in most of the programs that we write, I recommend that you study the move method next.
Recommended study trail: Return to the discussion of the method named rollAtSpeed.
Brief description: This method allows you to manually arrange the component objects that make up an object in the scene edit mode, save that arrangement of objects as a pose with a unique name, and then cause the object to assume that pose at runtime.
The end of the recommended study trail
Well, you've made it. If you have been following my recommended study trail, you have arrived at the last stop. And it may seem that I have saved the easiest method for last.
Creating a pose
Alice provides several mechanisms by which you can manually arrange the component parts of an object to suit your liking. For example, you might want to manually arrange the coach's arms above his head to replicate a football official's touchdown signal. Having done that, you might like to save this as a pose that can be used later in your program.
Although manually arranging the component parts of an object into a pose can be very difficult, saving and using the pose later is very easy.
Saving a pose
Once you have the object's component parts arranged into the pose, click the capture pose button in the details menu. Then enter a unique name for the pose in the text field that appears.
Using the pose
Later, to cause the object to assume that pose in your program, simply call the setPose method on your object passing the name of the pose as a parameter. The setPose method has one required parameter, which is the name of the pose. It also has the following two default parameters, which you already know all about:
The next stop on the recommended study trail
There are no more methods to be studied on the trail. I hope that by now you are sufficiently familiar with Alice's primitive methods that you can effectively use them in your animation programs. You may not remember all of the details. Just keep a link to this document handy so that you can find it when you need it to refresh your memory on any particular method.
From here, I recommend that you go to the section titled Run the programs.
Recommended study trail: Return to the explanation of the method named constrainToPointAt.
Brief description: A method to cause an object to re-orient itself so that its green axis becomes parallel to the green axis belonging to the world.
A very simple method
The standUp method is one of the simplest of the primitive methods. It has no required parameters. However, it does have the following default parameters:
If you accept the default values for the default parameters, the behavior of the method is relatively simple. The default parameters named duration and style don't add much complexity to the method. However, as is almost always the case, you can complicate the method's behavior by your choice of a non-default value for the parameter named asSeenBy.
Behavior of the standUp method
When the standUp method is called on an object, the default behavior is for that object to rotate itself as necessary to cause its green axis to become parallel to the green axis of the world.
On the other hand, if you specify some other object as the value of the asSeenBy property, the behavior of the standUp method is to cause the object on which the method is called to cause its green axis to be parallel to the green axis of the object that is specified as the value for the asSeenBy method.
Demonstrate by making interactive method calls
This method can probably best be demonstrated by making interactive method calls (see setPointOfView for instructions on how to make interactive method calls) and manipulating the object using the buttons in the upper right portion of the screen in the scene edit mode. I will walk you through some steps to demonstrate the default behavior and let you continue on your own to demonstrate the more complex behavior obtained by specifying some other method object as the value of the asSeenBy parameter.
Do the following to get started:
At this point, your screen should be very similar to Figure 40.
Figure 40. All objects aligned to the world in the program standUp01.
 |
Display the axes of the world, the ground, and the penguin
Select the ground in the object tree. The horizontal white line that you see in the center of the screen is the edge view of the snow-covered ground. The red axis shown on the left side of the screen is the red axis of the ground. It is aligned with the red axis of the world. The green axis shown at the top of the screen is the green axis of the ground, and it is aligned with the green axis of the world. The blue axis cannot be seen because it is protruding directly toward the camera lens and at most, would appear as a single blue pixel.
Select the penguin in the object tree to cause its axes to become visible. They should align with those of both the ground and the world. The most important thing to note at this point is that the green axis of the world points directly up.
Tumble the penguin
Select the Tumble Objects button in the upper right portion of the screen and tumble the penguin around a little producing something similar to Figure 41. It isn't critical what the viewpoint of the penguin turns out to be at this point as long as its green axis is not parallel to the green axis of the world.
Figure 41. Tumbled penguin in program named standUp01.
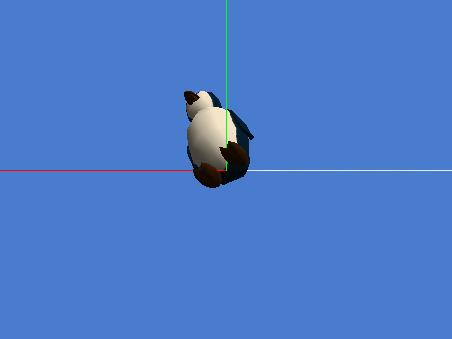 |
Call the standUp method on the penguin
Interactively call the standUp method on the penguin. This should cause it to rotate in such a way as to cause its green axis to point straight up again similar to that shown in Figure 40. However, it may or may not still be facing the camera. This depends on whether or not you turned it around its green axis while you were tumbling it.
Realign the penguin with the world
Now realign the penguin to the viewpoint of the world. Make interactive method calls to move the penguin down and to the left about one-half meter in both directions. The penguin's green axis should still be parallel to the green axis of the world and the penguin should be facing the camera.
Tumble the penguin again in this new position to cause its green axis to no longer be parallel to the green axis of the world. Then call the standUp method again on the penguin. Once again, the penguin will rotate itself as necessary to cause its green axis to be parallel to the green axis of the world.
Summary of default behavior
The default behavior of the standUp method should not change the position of the center point of the object on which it is called. I also believe that it should not rotate the object around its green axis in the process of standing the object up. Rather, all of the rotation necessary to cause the object's green axis to be parallel to the green axis of the world should involve rotation only around the red and blue axes.
Continue on your own
To learn more about the behavior of this method, place a flashlight in the world. Tumble the flashlight. Then write a simple program to call the standUp method on the penguin specifying the flashlight as the value of the asSeenBy parameter. Note the final orientation of the green axis of the penguin relative to the green axis of the flashlight.
The next stop on the recommended study trail
The explanation for the standUp method wasn't nearly as complicated as the explanations for some of the methods that were explained earlier. While we are discussing easy methods, I recommend that you study the method named say next.
Recommended study trail: Return to the discussion of the method named moveAwayFrom.
Brief description: A method to cause an object to move in a specified direction at a specified speed for a specified period of time. The time is specified by the parameter named duration, which has a default value of one second.
Speed, distance, and time
You probably learned in your high school physics course that average speed, distance, and time are related according to the algebraic equation shown in Figure 49.
Figure 49. Relationship among average speed, distance, and time.
|
where:
|
Since this is an algebraic equation involving the three variables speed, distance, and time, if you know the value of any two of the variables, you can easily compute the value of the third variable.
The moveAtSpeed method versus the move method
The purpose of this section is to explain and to illustrate the behavior of the method named moveAtSpeed. It will be beneficial to compare this method with the move method in order to understand the difference between the two.
Both methods have two required parameters, one of which is the direction of motion, so there is no difference with regard to this parameter.
Both methods have a default parameter named duration. You can either accept the default value of one second for this parameter, or you can specify a different value. This parameter specifies the length of time that will be required to complete the motion. Since the same default parameter appears in both methods with the same purpose in both cases, there is no difference between the methods with regard to the duration parameter either.
The all-important second required parameter
The difference between the two methods lies in the second of the two required parameters.
The move method requires you to specify the distance that the object will move, leaving speed as the unspecified value.
The moveAtSpeed method requires you to specify the speed at which the object will move, leaving distance as the unspecified value.
Must know two of the three values
To use either of the two methods effectively, the program must know (or accept the default value for) two of the three variables described in Figure 49. As mentioned earlier, if you know the values any two of the variables speed, distance, and time, you can always compute the value of the third. Given this, you should be able to accomplish anything with the move method that you can accomplish with the moveAtSpeed method, and vice versa.
However, depending on which two of the three variables are known, (or can be most easily computed), one of the methods will probably be easier to use than the other one in any specific application.
Description of the moveAtSpeed method
Given that explanation for starters, the moveAtSpeed method has two required parameters:
In addition, the moveAtSpeed method has the following default parameters:
These are the same default parameters as the default parameters for the move method, except that the move method also has a style default parameter.
You are already very familiar with the first two default parameters in the above list. As of this writing, I haven't investigated the default parameter named isScaledBySize, so I am unable to describe the behavior that it imparts to the method. In any event, it has a default value of false indicating that by default, it probably doesn't impart any behavior at all.
The program named moveAtSpeed02
The program named moveAtSpeed02 illustrates the use of the moveAtSpeed method to cause an airplane to:
Description of the program behavior
The program begins with the engine shut down and the prop not turning. The pilot starts the engine, causing the prop to start turning, and accelerates down the runway until the liftoff speed is reached. When the liftoff speed is reached, the pilot pulls back on the stick, causing the nose of the airplane to tilt upward which in turn causes the airplane to lift off the runway. The pilot retracts the landing gear at that point and the airplane continues to accelerate and climb until it reaches the other side of the screen.
Figure 50 shows a screen shot shortly after the pilot has started the engine and is accelerating down the runway.
Figure 50. Airplane starting down the runway in the program named moveAtSpeed02.
 |
Houston, we have liftoff
Figure 51 shown a screen shot at the point where the airplane has lifted off the runway and the pilot has retracted the landing gear.
Figure 51. Airplane lifting off the runway in the program named moveAtSpeed02.
 |
A successful flight
Figure 52 shows the airplane in an advanced state of climb.
Figure 52. Airplane continuing to climb in the program named moveAtSpeed02.
 |
Source code for the program named moveAtSpeed02
The source code for the program is shown in Listing 17.
No explanation should be needed
The moveAtSpeed method is called on the airplane (named T3A, which apparently is the model number of the airplane) about two-thirds of the way through the listing.
At this point on my recommended study trail, you should understand all of the code in Listing 17, so no explanation of that code should be necessary.
The next stop on the recommended study trail
You are really getting close to the end of the trail now. There are only three more methods to be covered on the trail, and the next two are very similar to this method named moveAtSpeed. I recommend that you study the method named turnAtSpeed next.
Recommended study trail: Return to the discussion of the method named moveAtSpeed.
Brief description: The turnAtSpeed and rollAtSpeed methods cause an object to rotate around one of its three axes in a specified direction at a specified rotational speed for a specified period of time. The time is specified by the parameter named duration, which has a default value of one second.
Very similar to the moveAtSpeed method
The turnAtSpeed and rollAtSpeed methods are very similar to one another and are both very similar to the method named moveAtSpeed. Therefore, I have combined the explanation of the two methods in this section.
If you were to copy the material from the explanation of the moveAtSpeed method and modify it so that it would apply to rotational motion instead of linear motion, you would have appropriate text for this section. For that reason, I will have very little to say about these two methods. Instead I will simply refer you to that earlier section.
Method parameters
Just as in the case of the earlier method named moveAtSpeed, each of these two methods has two required parameters:
In addition, each of these methods has the following default parameters (one less than the default parameters for the moveAtSpeed method):
You are familiar with both of these default parameters because we have used them in numerous sample programs on the recommended study trail.
The program named turnAtSpeed01
I began developing this program simply to illustrate the use of the turnAtSpeed method to cause a shark to circle in the water at a non-uniform rate. Then I decided I needed tasty morsel for the shark to be circling around, so I put a hare in the water. Well, to make a long story short, I kept adding features until I had spent several hours developing this animation program.
The basic animation is that of a shark circling a hapless hare in the water. The whole thing is being photographed by a video camera circling in a news helicopter overhead.
The speed at which the shark and the helicopter circle their prey varies with time on the basis of a random number generator. The hapless hare is bobbing up and down in the water frantically waving his arms (front paws) and his ears.
Sometimes the shark is completely submerged. Sometimes only his dorsal fin can be seen circling the hare, and sometimes he breaks out of the water completely and glides in the air for a short distance before slipping back into the water.
However, the shark must not really be hungry because the hare never gets eaten by the shark.
Two screen shots
Two screen shots taken from this program are shown in Figures 53 and 54.
Figure 53 shows a shot where the shark is partially out of the water.
Figure 53. Shark partially out of the water in program turnAtSpeed01.
 |
Figure 54 shows a shot where only the shark's dorsal fin is showing above the surface of the water.
Figure 54. Only the dorsal fin showing in program turnAtSpeed01.
 |
Source code for program turnAtSpeed01
Listing 18 shows the source code for this program.
Long and tedious code
While this program is rather long and tedious, there is nothing in it that should be new to those of you who have been following my recommended study trail. Therefore, I won't provide an explanation of the program.
The last stop on the recommended study trail
The next and last method on the recommended study trail is the method named setPose.
See the section titled The turnAtSpeed and rollAtSpeed methods for an explanation of both methods.
Recommended study trail: Return to the explanation of the methods named pointAt and turnToFace.
Brief description: Similar to the method named pointAt, but the differences are too complicated to be described in a couple of sentences. See the text that follows for a discussion of how the two methods differ.
A first cousin of the pointAt method
The method named constrainToPointAt is a first cousin of the method named pointAt, but there are significant differences between the two. I can't think of any better way to explain the behavior of the constrainToPointAt method than to compare it with the behavior of the pointAt method.
Partial listing of program named constrainToPointAt01
I will make this comparison using a modified version of the program named pointAt01, which I presented in Listing 8, and which I explained in the section on the pointAt method.
This new program, named constrainToPointAt01 is identical to the earlier program with the exception of the code in the code block identified by the comment that reads "Begin animation." Therefore, to save space, I will show you only the new version of the animation block. To write (or download) this program, simply save the earlier program in a new world named constrainToPointAt01, and then make the changes shown in the animation block in Listing 9.
Three method calls
The code in Listing 9 begins with the following three method calls in sequence:
Behavior of each of the three method calls
Two of the method calls are disabled and one is enabled in Listing 9. You can see the differences in behavior between the three by enabling any one of the method calls (while disabling the other two) and playing the world.
First call identical to earlier program
The first method call listed above is identical to the method call used in the earlier program named pointAt01. As you will recall from that program, the camera is initially facing the northeast and the airplane arrives from the north on a heading that is a few degrees east of south. When the program starts running, the camera swings around to its left and pitches upward slightly in order to lock the targeting circle onto the airplane. Although it doesn't take very long for this to happen, some time is required for the camera to initially lock onto the target, and this is very realistic for this scenario. The camera remains locked onto the airplane until the airplane disappears over the southern horizon.
Overall behavior of the program named pointAt01
The overall behavior of the earlier program that used the first method call listed above is shown in the four screen shots in Figures 28 through 31. Note in particular how the horizon is tilted in some of these screen shots indicating that the camera executed some roll in addition to yaw and pitch in order to maintain the lock on the target.
Also note that in order to achieve the desired result using the pointAt method, it was necessary for me to specify the value of the parameter named asSeenBy to be the camera. Specifying any other value, including <none> would not do the job.
Although it wasn't necessary to specify that the style should begin and end abruptly, that specification did seem to make the action more realistic.
Using the constrainToPointAt method
|
Listing 9 shows the call to the method named constrainToPointAt enabled and the other two method calls disabled.
Note that this method call is somewhat simpler than the call to the pointAt method that I described above. For example, the default value of <none> was accepted for the parameter named asSeenBy. Also, there was no specification of a value for the style parameter. In fact, this method does not allow a specification for the style parameter (see sidebar).
Acquires the target instantly
If you download and play this world with the constrainToPointAt method enabled and compare it with the behavior of the pointAt method discussed above, the first major difference that you will notice is that the constrainToPointAt method acquires the target instantly as soon as the program starts running.
Even though the camera is initially facing 45 degrees east of the target airplane, there is no visual indication of the camera swinging around to acquire a lock on the airplane that is arriving from the north. In some scenarios that would be a good thing. In this scenario however, it is less realistic. In the real world, the mass of the anti-aircraft gun would require some time for it to swing around and acquire the lock on the target.
Compare the two programs
For comparison purposes, Figures 36 through 39 show screen shots taken for this program at approximately the same points in the animation as the screen shots shown in Figures 28 through 31. Those earlier screen shots were taken from the program named pointAt01, which used a call to the pointAt method instead of a call to the constrainToPointAt method.
Figure 36. Early screenshot of the program named constrainToPointAt01.
 |
These two screen shots are very similar
Except for the fact that I wasn't quick enough to catch the airplane in exactly the same point in its roll, there isn't much difference between Figure 36 and the earlier Figure 28.
Figure 37. Airplane passing overhead in program named constrainToPointAt01.
 |
There is a significant difference between Figure 37 and Figure 29. Can you spot it?
No roll required
The horizon in Figure 37 is completely flat whereas the horizon in Figure 29 is tilted. This indicates that the camera executed a slight roll in order to maintain the lock as the airplane passed overhead (and slightly to the east) when the method named pointAt was used to track the target.
The fact that the horizon is still perfectly flat in Figure 37 indicates that the constrainToPointAt method is able to accomplish the same thing without the requirement to roll the camera. Whether or not this is a good thing is strictly a judgment call based on the scenario being modeled in the animation.
Although I know absolutely nothing about anti-aircraft guns, the surface mounted guns that I have seen in movies about World War II probably didn't have the ability to roll, so in this case, the situation shown in Figure 37 is probably more realistic than the situation shown in Figure 29.
Figure 38. Airplane has passed overhead in program named constrainToPointAt01.
 |
Again, no requirement to roll the camera
The main difference between Figure 38 and Figure 30 seems to be the lack of a requirement to roll the camera in order to track the airplane in Figure 38.
Figure 39. Airplane flies away in program named constrainToPointAt01.
 |
Similarly, the main difference between Figure 39 and Figure 31 is once again the lack of a requirement for the method named constrainToPointAt to roll the camera in order to track the airplane in Figure 39.
Which is the most realistic?
In the scenario of a surface-mounted anti-aircraft gun, neither approach is perfect. However, I would have to vote for the use of the pointAt method instead of the constrainToPointAt method because I believe that it is more realistic. The immediate acquisition of the target airplane at the beginning of the run by the constrainToPointAt method could be a very good thing in some scenarios, but in this scenario, it looks a lot more realistic for the camera to swing around to the left by about 45 degrees in order to acquire the target.
On the other hand, I don't believe that the requirement for the pointAt method to roll the camera in order to maintain the lock is very good for a surface-mounted World War II vintage anti-aircraft gun. On the other hand, it might be excellent for a gun on a space ship being used to track and shoot at other space ships. After all, no one knows exactly how such a space gun would behave anyway.
Neither approach is perfect
Neither approach is perfect for this scenario, but at least you now know about some of the differences in behavior between the two methods, and you will be able to make an informed choice between them in your scenarios.
Oops, I almost forgot
I almost forgot the third possibility shown in the code in Listing 9. This possibility, which is disabled in Listing 9, is to use a call to the pointAt method that has been simplified down to the level of the call to the constrainToPointAt method immediately above it. The bottom line on this method call is that it simply doesn't work. If you enable this method and play the world, you will see that it doesn't successfully acquire the target airplane until the airplane is completely out of range flying away to the south.
And your choices are...
For this animation scenario, you have two choices (and possibly others that I haven't illustrated). You can use a very simple call to the constrainToPointAt method, or a more complicated call to the pointAt method. Neither is perfect, but both get the job done reasonably well. Each has advantages and disadvantages relative to the other.
The next stop on the recommended study trail
The two programs discussed in this section illustrate the similarities and the differences between the pointAt method and the constrainToPointAt method. This material, and most of the material up to this point on the recommended study trail, is fairly deep and sometimes complicated.
It's time to give you a break and let you study something easy. For that purpose, I recommend that you study the method named standUp next.
I encourage you to use the source code listings that I have provided to write (or download) and run the animation programs. Experiment with them. Make changes and observe the results. Above all, have some fun in the process.
This appendix provides detailed explanations of the behavior of each of the twenty primitive methods in Alice and in most cases provides sample code to illustrate that behavior.
Listing 1. Source code for the program named move01.
move01's CodeCreated by: Dick BaldwinworldEvents
Methods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 2. Source code for the program named roll01.
roll01's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 3. Source code for the program named roll02.
roll02's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 4. Source code for the program named roll03.
roll03's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 5. Source code for program named turn01.
turn01's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 6. Source code for the program named turn02.
turn02's Code
Created by: Dick Baldwin
world
Methods
public void main ( ) {
// Brief description of program.
doInOrder {
// This program illustrates the turn method.
// In this program an airplane turns around the
// red axis of a blimp whose red axis is perpendicular
// to the red axis of the airplane. This takes place
// while flying toward the camera, and it looks more
// like a roll than a turn.
}
// Make all of the objects invisible.
doInOrder { . . . }
ground .set( isShowing , false ); duration = 0 seconds
airplane .set( isShowing , false ); duration = 0 seconds
blimp .set( isShowing , false ); duration = 0 seconds
}
// Set viewpoint of the camera and the ground.
doInOrder { . . . . . . }
camera .setPointOfView( world ); duration = 0 seconds
// Turn camera to face north
camera .turn( LEFT , 0.5 revolutions ); duration = 0 seconds
// Get some altitude.
camera .move( UP , 20 meters ); duration = 0 seconds
ground .setPointOfView( world ); duration = 0 seconds
}
// Set viewpoint of the airplane.
doInOrder { . . . . . }
airplane .setPointOfView( world ); duration = 0 seconds
// Get some altitude.
airplane .move( UP , 20.3 meters ); duration = 0 seconds
// Get into position.
airplane .move( BACKWARD , 10 meters ); duration = 0 seconds
}
// Set viewpoint of blimp.
doInOrder { . . . . . . . }
// Make red axis of blimp perpendicular to the
// red axis of the airplane and 0.3 meters
// below it.
blimp .setPointOfView( world ); duration = 0 seconds
blimp .move( UP , 20 meters ); duration = 0 seconds
blimp .move( BACKWARD , 10 meters ); duration = 0 seconds
blimp .turn( LEFT , 0.25 revolutions ); duration = 0 seconds
}
// Make all objects visible.
doInOrder { . . . }
ground .set( isShowing , true ); duration = 0 seconds
airplane .set( isShowing , true ); duration = 0 seconds
blimp .set( isShowing , true ); duration = 0 seconds
}
// Perform animation
doTogether {
airplane .move( FORWARD , 9 meters ); duration = 15 seconds style = BEGIN_GENTLY_AND_END_ABRUPTLY
airplane .turn( FORWARD , 2 revolutions ); duration = 15 seconds asSeenBy = blimp
} }
Listing 7. Source code for the program named turn03.
turn03's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 8. The source code for the program named pointAt01.
pointAt01's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 9. Partial listing of program named constrainToPointAt01.
| // Begin animation | |
| doTogether { | |
| // Call pointAt when enabled. | |
| |
|
| // Call constrainToPointAt when enabled. | |
| camera .constrainToPointAt( airplane ); duration = 30 seconds | |
| // Call pointAt when enabled. | |
| |
|
| // Airplane arrives from due north, rolling. | |
| airplane .move( FORWARD , 30 meters ); duration = 30 seconds style = BEGIN_AND_END_ABRUPTLY | |
| airplane .roll( RIGHT , 4 revolutions ); duration = 30 seconds | |
| } | |
Listing 10. Source code for the program named say01.
say01's CodeCreated by: Dick BaldwinworldMethods
|
||
Listing 11. Source code for program named resize01.
resize01's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||
Listing 12. Source code for the program named orientTo01.
orientTo01's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 13. Source code for the program named moveTo01.
moveTo01's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 14. Source code for the program named moveTo02.
moveTo02's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||
Listing 15. Source code for the program named moveToward01.
moveToward01's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 16. Source code for the program named moveAwayFrom01.
moveAwayFrom01's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 17. Source code for the program named moveAtSpeed02.
MoveAtSpeed02's CodeCreated by: Dick BaldwinworldMethods
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Listing 18. Source code for program turnAtSpeed01.
turnAtSpeed01's CodeCreated by: Dick BaldwinworldMethods
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Copyright 2007, Richard G. Baldwin. Faculty and staff of public and private non-profit educational institutions are granted a license to reproduce and to use this material for purposes consistent with the teaching process. This license does not extend to commercial ventures. Otherwise, reproduction in whole or in part in any form or medium without express written permission from Richard Baldwin is prohibited.
Richard has participated in numerous consulting projects and he frequently provides onsite training at the high-tech companies located in and around Austin, Texas. He is the author of Baldwin's Programming Tutorials, which have gained a worldwide following among experienced and aspiring programmers. He has also published articles in JavaPro magazine.
In addition to his programming expertise, Richard has many years of practical experience in Digital Signal Processing (DSP). His first job after he earned his Bachelor's degree was doing DSP in the Seismic Research Department of Texas Instruments. (TI is still a world leader in DSP.) In the following years, he applied his programming and DSP expertise to other interesting areas including sonar and underwater acoustics.
Richard holds an MSEE degree from Southern Methodist University and has many years of experience in the application of computer technology to real-world problems.
-end-